Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T13:13:46.338Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE ARITHMETIC OF MORI MONOIDS AND DOMAINS

Part of: Semigroups Arithmetic rings and other special rings General commutative ring theory

Published online by Cambridge University Press:  08 April 2019

QINGHAI ZHONG Open the ORCID record for QINGHAI ZHONG [Opens in a new window]
QINGHAI ZHONG*
Affiliation:
University of Graz, NAWI Graz, Institute for Mathematics and Scientific Computing, Heinrichstrasse 36, 8010 Graz, Austria e-mail: [email protected]; https://imsc.uni-graz.at/zhong/
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a Mori domain with complete integral closure 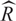$\widehat R$, nonzero conductor 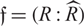$\mathfrak f = (R: \widehat R)$, and suppose that both v-class groups 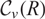${{\cal C}_v}(R)$ and 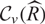${{\cal C}_v}(3\widehat R)$ are finite. If 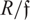$R \mathfrak f$ is finite, then the elasticity of R is either rational or infinite. If 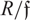$R \mathfrak f$ is artinian, then unions of sets of lengths of R are almost arithmetical progressions with the same difference and global bound. We derive our results in the setting of v-noetherian monoids.

MSC classification

Primary: 13A05: Divisibility; factorizations
Secondary: 13F05: Dedekind, Prüfer, Krull and Mori rings and their generalizations 20M13: Arithmetic theory of monoids
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 2 , May 2020 , pp. 313 - 322
Copyright
Copyright © Glasgow Mathematical Journal Trust 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D. D. and Anderson, D. F., Elasticity of factorizations in integral domains, J. Pure Appl. Algebra 80 (1992), 217–235.CrossRefGoogle Scholar
Anderson, D. F., Elasticity of factorizations in integral domains: A survey, Factorization in Integral Domains, Lect. Notes Pure Appl. Math., vol. 189 (Marcel Dekker, New York, 1997), 1–29.Google Scholar
Baginski, P. and Chapman, S. T., Arithmetic Congruence Monoids: A Survey, Combinatorial and Additive Number Theory: CANT 2011 and 2012, in Proceedings in Mathematics and Statistics, vol. 101 (Springer, New York, 2014), 15–38.Google Scholar
Barucci, V., Mori domains, in Non-Noetherian Commutative Ring Theory, Mathematics and Its Applications, vol. 520 (Kluwer Academic Publishers, Dordrecht, 2000), 57–73.10.1007/978-1-4757-3180-4_3CrossRefGoogle Scholar
Chapman, S. T., Fontana, M., Geroldinger, A., and Olberding, B. (Editors), Multiplicative Ideal Theory and Factorization Theory, in Proceedings in Mathematics and Statistics, vol. 170 (Springer, Cham, 2016).Google Scholar
Cziszter, K., Domokos, M. and Geroldinger, A., The interplay of invariant theory with multiplicative ideal theory and with arithmetic combinatorics, in Multiplicative Ideal Theory and Factorization Theory (Springer, Cham, 2016), 43–95.CrossRefGoogle Scholar
Fan, Y., Geroldinger, A., Kainrath, F. and Tringali, S., Arithmetic of commutative semigroups with a focus on semigroups of ideals and modules, J. Algebra Appl. 11 (2017), 1750234 (42 pages).CrossRefGoogle Scholar
Fontana, M., Frisch, S., Glaz, S., Tartarone, F., and Zanardo, P. (Editor), Rings, polynomials, and modules (Springer, Cham, 2017).CrossRefGoogle Scholar
Gao, W. and Geroldinger, A., On products of k atoms, Monatsh. Math. 156 (2009), 141–157.Google Scholar
Geroldinger, A., Sets of lengths, Am. Math. Monthly 123 (2016), 960–988.CrossRefGoogle Scholar
Geroldinger, A. and Halter-Koch, F., Congruence monoids, Acta Arith.112 (2004), 263–296.CrossRefGoogle Scholar
Geroldinger, A. and Halter-Koch, F., Non-Unique Factorizations. Algebraic, Combinatorial and Analytic Theory, in Pure and Applied Mathematics, vol. 278 (Chapman & Hall/CRC, Boca Raton, 2006).Google Scholar
Geroldinger, A. and Hassler, W., Arithmetic of Mori domains and monoids, J. Algebra 319 (2008), 3419–3463.CrossRefGoogle Scholar
Geroldinger, A. and Hassler, W., Local tameness of v-noetherian monoids, J. Pure Appl. Algebra 212 (2008), 1509–1524.CrossRefGoogle Scholar
Geroldinger, A. and Zhong, Q., Long sets of lengths with maximal elasticity, Can. J. Math.70 (2018), 1284–1318.CrossRefGoogle Scholar
Geroldinger, A., Ramacher, S. and Reinhart, A., On v-Marot Mori rings and C-rings, J. Korean Math. Soc. 52 (2015), 1–21.CrossRefGoogle Scholar
Gotti, F., On the system of sets of lengths and the elasticity of submonoids of $\mathbb{N}^d$, https://arxiv.org/abs/1806.11273.Google Scholar
Halter-Koch, F., Ideal Systems. An Introduction to Multiplicative Ideal Theory (Marcel Dekker, 1998).Google Scholar
Kainrath, F., Elasticity of finitely generated domains, Houston J. Math.31 (2005), 43–64.Google Scholar
Kainrath, F., Arithmetic of Mori domains and monoids: The global case, Multiplicative Ideal Theory and Factorization Theory, in Springer Proc. Math. Stat., vol. 170 (Springer, Cham, 2016), 183–218.Google Scholar
Reinhart, A., On integral domains that are C-monoids, Houston J. Math. 39 (2013), 1095–1116.Google Scholar
Schmid, W. A., Some recent results and open problems on sets of lengths of Krull monoids with finite class group, Multiplicative Ideal Theory and Factorization Theory, in Springer Proc. Math. Stat., vol. 170 (Springer, Cham, 2016), 323–352.Google Scholar
Tringali, S., Structural properties of subadditive families with applications to factorization theory, Israel J. Math. (to appear), https://arxiv.org/abs/1706.03525.Google Scholar
Zhong, Q., On elasticities of locally finitely generated monoids, https://arxiv.org/abs/1807.11523.Google Scholar