Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T17:11:53.908Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOLVABILITY OF CERTAIN EQUATIONS OF ARBITRARY LENGTH OVER TORSION-FREE GROUPS

Part of: Low-dimensional topology Special aspects of infinite or finite groups

Published online by Cambridge University Press:  13 October 2020

MUHAMMAD FAZEEL ANWAR ,
MAIRAJ BIBI  and
MUHAMMAD SAEED AKRAM
MUHAMMAD FAZEEL ANWAR
Affiliation:
Department of Mathematics, Sukkur IBA University, e-mail:[email protected]
MAIRAJ BIBI
Affiliation:
Department of Mathematics, COMSATS University, Islamabad, Pakistan, e-mail:[email protected]
MUHAMMAD SAEED AKRAM
Affiliation:
Department of Mathematics, Khawaja Fareed UEIT, e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a nontrivial torsion-free group and 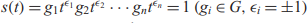$s\left( t \right) = {g_1}{t^{{\varepsilon _1}}}{g_2}{t^{{\varepsilon _2}}} \ldots {g_n}{t^{{\varepsilon _n}}} = 1\left( {{g_i} \in G,{\varepsilon_i} = \pm 1} \right)$ be an equation over G containing no blocks of the form 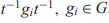${t^{- 1}}{g_i}{t^{ - 1}},{g_i} \in G$. In this paper, we show that 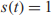$s\left( t \right) = 1$ has a solution over G provided a single relation on coefficients of s(t) holds. We also generalize our results to equations containing higher powers of t. The later equations are also related to Kaplansky zero-divisor conjecture.

MSC classification

Primary: 20F05: Generators, relations, and presentations
Secondary: 57M07: Topological methods in group theory
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 3 , September 2021 , pp. 651 - 659
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibi, M. and Edjvet, M., Equation of length seven over torsion-free groups, J. Group Theory 21 (2018), 147–164.CrossRefGoogle Scholar
Bibi, M., Anwar, M. F., Iqbal, S. and Akram, M. S., The solution of length eight equations over torsion free groups, Preprint.Google Scholar
Bogley, W. A. and Pride, S. J., Aspherical relative presentations, Proc. Edinburgh Math. Soc. 35 (1992), 1–39.CrossRefGoogle Scholar
Brodski, S. D. and Howie, J., One-relator products of torsion-free groups, Glasg. Math. J. 35(1) (1993), 99–104.CrossRefGoogle Scholar
Clifford, A. and Goldstein, R. Z., Equations with torsion-free coefficients, Proc. Edinburgh Math. Soc. 43(2) (2000), 295–307.CrossRefGoogle Scholar
Evangelidou, A., The solution of length five equations over groups, Comm. Alg. 35 (2007), 1914–1948.CrossRefGoogle Scholar
Ivanov, S.V. and Klyachko, A. A., Solving equations of length at most six over torsion-free groups, J. Group Theory 3(3) (2000), 329–337.CrossRefGoogle Scholar
Kim, S. K., On the asphericity of length-6 relative presentations with torsion-free coefficients, Proc. Edinburgh Math. Soc. 51(1) (2008), 201–214.CrossRefGoogle Scholar
Levin, F., Solutions of equations over groups, Bull. Amer. Math. Soc. 68 (1962), 603–604.CrossRefGoogle Scholar
Prishchepov, M. I., On small length equations over torsion-free groups, Internat. J. Algebra Comput. 4(4) (1994), 575–589.CrossRefGoogle Scholar
Stallings, J. R., A graph theoretic lemma and group embedding, Ann. Math. Stud. 111 (1987), 145–155.Google Scholar