Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T08:56:24.295Z Has data issue: false hasContentIssue false
  • English
  • Français

On residually transcendental valued function fields of conics

Published online by Cambridge University Press:  18 May 2009

Sudesh K. Khanduja
Sudesh K. Khanduja
Affiliation:
Centre for Advanced Study in Mathematics, punjab University, Chandigarh 160014, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K/Kobe a finitely generated field extension of transcendence degree 1. Let u0 be a valuation of Koand v a valuation of Kextending v0such that the residue field of vis a transcendental extension ofthe residue field k0of vo/such a prolongation vwill be called a residually transcendental prolongation of v0. Byan element with the uniqueness propertyfor (K, v)/(K0, v0) (or more briefly for v/v0)we mean an element / of Khaving u-valuation 0 which satisfies (i) the image of tunder the canonicalhomomorphism from the valuation ring of vonto the residue field of v(henceforth referred to as the v-residue ot t) is transcendental over ko; that is vcoincides with the Gaussian valuation 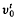on the subfield K0(t) defined by 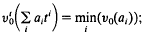(ii) vis the only valuation of K (up to equivalence) extending the valuation .

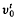Type
Research Article
Information
Glasgow Mathematical Journal , Volume 38 , Issue 2 , May 1996 , pp. 137 - 145
Copyright
Copyright © Glasgow Mathematical Journal Trust 1996

References

REFERENCES

1.Artin, E., Algebraic numbers and algebraic functions (Gordon and Breach, New York 1967).Google Scholar
2.Bourbaki, N., Commutative algebra, Chapter 6 (Hermann Publishers in Arts and Science, 1972).Google Scholar
3.Endler, O., Valuation theory (Springer-Verlag, 1972).CrossRefGoogle Scholar
4.Fresnel, J. and Matignon, M., Sur les espaces analytiques quasicompacts de dimension 1 sur un corps value complet, ultrametrique, Annali di Mathematica pura ed applicata (4), 145 (1986), 159–210.CrossRefGoogle Scholar
5.Khanduja, S. K., On valuations of K(x), Proc. Edinburgh Math. Soc. 35 (1992), 419–426.CrossRefGoogle Scholar
6.Lang, S., Introduction to algebraic geometry (Interscience publishers, 1964).Google Scholar
7.Matignon, M., Genre et genre residual des corps de fonctions values, Manuscripta Math. 58 (1987), 179–214.CrossRefGoogle Scholar
8.Matignon, M. and Ohm, J., A structure theorem for simple transcendental extensions of valued fields, Proc. Amer. Math. Soc. 104 (1988), 392–402.CrossRefGoogle Scholar
9.Matignon, M. and Ohm, J., Simple transcendental extensions of valued fields III: The uniqueness property, J. Math. Kyoto Univ., 30 (1990), 347–365.Google Scholar
10.Ohm, J., Simple transcendental extensions of valued fields, J. Math. Kyoto Univ.,22 (1982), 201–221.Google Scholar
11.Ohm, J., Function fields of conies, a theorem Amitsur-MacRae and a problem of Zariski, in Algebraic geometry and its applications, (Springer-Verlag, 1994), 333–363.CrossRefGoogle Scholar
12.Polzin, M., Prolongement de la valeur absolue de Gauss et probleme de Skolem, Bull. Soc. Math. France 116 (1988), 103–132.CrossRefGoogle Scholar
13.Waerden, B. L. van der, Modern algebra 1 (Ungar, New York, 1964).Google Scholar