Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dursun, Ugur
1999.
On minimal and Chen immersions in space forms.
Journal of Geometry,
Vol. 66,
Issue. 1-2,
p.
104.
Arslan, Kadri
Bayram, Bengü
Bulca, Betül
and
Öztürk, Günay
2012.
Generalized Rotation Surfaces in $${\mathbb E^4}$$.
Results in Mathematics,
Vol. 61,
Issue. 3-4,
p.
315.
GANCHEV, GEORGI
and
MILOUSHEVA, VELICHKA
2015.
SPECIAL CLASSES OF MERIDIAN SURFACES IN THE FOUR-DIMENSIONAL EUCLIDEAN SPACE.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 6,
p.
2035.


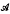 -submanifold (Chen submanifold) to an
-submanifold (Chen submanifold) to an 