No CrossRef data available.
Article contents
On Prefrattini residuals†
Published online by Cambridge University Press: 18 May 2009
Extract
All groups considered in the sequel are finite. Let (ℭ and 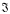 denote the formations of groups which consist of collections of groups that respectively either split over each normal subgroup (nC-groups) or for which the groups do not possess nontrivial Frattini chief factors [8]. The purpose of this article is to develop and expand a concept that arises naturally with the residuals for these formations, namely each G-chief factor
denote the formations of groups which consist of collections of groups that respectively either split over each normal subgroup (nC-groups) or for which the groups do not possess nontrivial Frattini chief factors [8]. The purpose of this article is to develop and expand a concept that arises naturally with the residuals for these formations, namely each G-chief factor 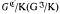 is non-complemented (Frattini). With respect to a solid set X of maximal subgroups, these properties are generalized respectively to so-called X-parafrattini (X-profrattini) normal subgroups for which each type is closed relative to products. The relationships among the unique maximal normal subgroups that result from these products, the solid set of maximal subgroups X, X-prefrattini subgroups, and the residuals of formations are explored. This leads to a well-defined collected of formations, the partially nonsaturated formations, with properties analogous to those which are totally non-saturated. In the development, attention is given to a set of maximal subgroups which is the image of a solid function defined on all groups, a weaker condition than that of a solid set. A result of particular interest answers affirmatively the long-standing conjecture that a non-trivial nC-group G is solvable if and only if each G-chief factor is complemented by a maximal subgroup. This will force a critical re-examination of the classification problem for nC-groups. Since the article continues the investigations on finite groups initiated in [2], a familiarity with that article is assumed. All other notation and terminology is from [6]. If M is a maximal subgroup of a group G and G/C or e G(M) is a monolithic primitive group, i.e. a group with a unique minimal normal subgroup, then M is called a monolithic maximal subgroupof G.
is non-complemented (Frattini). With respect to a solid set X of maximal subgroups, these properties are generalized respectively to so-called X-parafrattini (X-profrattini) normal subgroups for which each type is closed relative to products. The relationships among the unique maximal normal subgroups that result from these products, the solid set of maximal subgroups X, X-prefrattini subgroups, and the residuals of formations are explored. This leads to a well-defined collected of formations, the partially nonsaturated formations, with properties analogous to those which are totally non-saturated. In the development, attention is given to a set of maximal subgroups which is the image of a solid function defined on all groups, a weaker condition than that of a solid set. A result of particular interest answers affirmatively the long-standing conjecture that a non-trivial nC-group G is solvable if and only if each G-chief factor is complemented by a maximal subgroup. This will force a critical re-examination of the classification problem for nC-groups. Since the article continues the investigations on finite groups initiated in [2], a familiarity with that article is assumed. All other notation and terminology is from [6]. If M is a maximal subgroup of a group G and G/C or e G(M) is a monolithic primitive group, i.e. a group with a unique minimal normal subgroup, then M is called a monolithic maximal subgroupof G.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1998


