Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Srinivasan, S
1991.
On orders solely of abelian groups, III.
Journal of Number Theory,
Vol. 39,
Issue. 2,
p.
175.


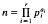 be the factorization of an integer
be the factorization of an integer 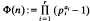 . In particular, for squarefree
. In particular, for squarefree