No CrossRef data available.
Article contents
On images and inverse images of Weierstrass points†
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The classical theory of Weierstrass points on a compact Riemann surface is well-known (see, for example, [3]). Ogawa [6] has defined generalized Weierstrass points. Let Y denote a compact complex manifold of (complex) dimension n. Let E denote a holomorphic vector bundle on Y of rank q. Let Jk(E) (k = 0, 1, …) denote the holomorphic vector bundle of k-jets of E [2, p. 112]. Put rk(E) = rank Jk(E) = q.(n + k)!/n!k!. Suppose that Γ(E), the vector space of global holomorphic sections of E, is of dimension γ(E)>0. Consider the trivial bundle Y × Γ(E) and the map
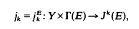
which at a point Q∈Y takes a section of E to its k-jet at Q. Put μ = min(γ(E),rk(E)).
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1978
References
REFERENCES
1.Altman, A. and Klciman, S., Introduction to Grothendieck duality theory, Lecture Notes in Mathematics No. 146 (Springer-Verlag, 1970).CrossRefGoogle Scholar
2.Golubitsky, M. and Guillemin, V., Stable mappings and their singularities (Springer-Verlag, 1973).Google Scholar
3.Gunning, R. C., Lectures on Riemann surfaces (Princeton University Press, Princeton, N.J., 1966).Google Scholar
4.Hirzebruch, F., Topological methods in algebraic geometry, Third edition (Springer-Verlag, 1966).Google Scholar
5.Lax, R. F., Weierstrass points of products of Riemann surfaces, Pacific J. Math. 66 (1976), 191–194.CrossRefGoogle Scholar
6.Ogawa, R. H., On the points of Weierstrass in dimension greater than one, Trans. Amer. Math. Soc. 184 (1973), 401–417.CrossRefGoogle Scholar
7.Rauch, H. E. and Farkas, H. M., Theta functions with applications to Riemann surfaces (Williams and Wilkins, Baltimore, 1974).Google Scholar
You have
Access