Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-05-02T19:48:47.058Z Has data issue: false hasContentIssue false
  • English
  • Français

On hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ and 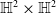$\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor

Part of: Global differential geometry Local differential geometry

Published online by Cambridge University Press:  30 April 2025

Qianshun Cui Open the ORCID record for Qianshun Cui [Opens in a new window] ,
Zejun Hu Open the ORCID record for Zejun Hu [Opens in a new window] ,
Xiaoge Lu Open the ORCID record for Xiaoge Lu [Opens in a new window]  and
Zeke Yao Open the ORCID record for Zeke Yao [Opens in a new window]
Qianshun Cui*
Affiliation:
School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, People’s Republic of China
Zejun Hu
Affiliation:
School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, People’s Republic of China
Xiaoge Lu
Affiliation:
School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, People’s Republic of China
Zeke Yao
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou, People’s Republic of China
*
Corresponding author: Qianshun Cui; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate hypersurfaces of 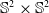$\mathbb{S}^2\times \mathbb{S}^2$ and 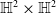$\mathbb{H}^2\times \mathbb{H}^2$ with recurrent Ricci tensor. As the main result, we prove that a hypersurface in 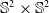$\mathbb{S}^2\times \mathbb{S}^2$ (resp. 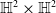$\mathbb{H}^2\times \mathbb{H}^2$) with recurrent Ricci tensor is either an open part of 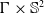$\Gamma \times \mathbb{S}^2$ (resp. 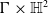$\Gamma \times \mathbb{H}^2$) for a curve $\Gamma$ in $\mathbb{S}^2$ (resp. $\mathbb{H}^2$), or a hypersurface with constant sectional curvature. The latter has been classified by H. Li, L. Vrancken, X. Wang, and Z. Yao very recently.

Keywords

Recurrent Ricci tensorRicci eigenvaluesconstant sectional curvaturenon-Hopf hypersurfacessemi-parallel Ricci tensor

MSC classification

Primary: 53B25: Local submanifolds
Secondary: 53C30: Homogeneous manifolds 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 21
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Castro, I. and Urbano, F., Minimal Lagrangian surfaces in $\mathbb{S}^2\times \mathbb{S}^2$ , Comm. Anal. Geom. 15(2) (2007), 217–248.CrossRefGoogle Scholar
Cho, J. T., Hamada, T. and Inoguchi, J. I., On three dimensional real hypersurfaces in complex space forms, Tokyo J. Math. 33(1) (2010), 31–47.CrossRefGoogle Scholar
Cui, Q. and Hu, Z., Nonexistence of non-Hopf Ricci-semisymmetric real hypersurfaces in $\mathbb{C}P^2$ and $\mathbb{C}H^2$ , Canad. Math. Bull. 67(1) (2024), 188–200.CrossRefGoogle Scholar
Gao, D., Hu, Z., Ma, H. and Yao, Z., On real hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ , Proc. Amer. Math. Soc. 150(10) (2022), 4447–4461.Google Scholar
Gao, D., Ma, H. and Yao, Z., On hypersurfaces of $\mathbb{H}^2\times \mathbb{H}^2$ , Sci. China Math. 67(2) (2024), 339–366.CrossRefGoogle Scholar
Gao, D., Van der Veken, J., Wijffels, A. and Xu, B., Lagrangian Surfaces in $\mathbb{H}^2\times \mathbb{H}^2$ , Comm. Anal. Geom. arXiv: 2106.13975v1.Google Scholar
Hu, Z. and Lu, X., On real hypersurfaces in $\mathbb{S}^2\times \mathbb{S}^2$ and $\mathbb{H}^2\times \mathbb{H}^2$ with parallel normal Jacobi operator, Mediterr. J. Math. 21(4) (2024), 16.Art. 133.CrossRefGoogle Scholar
Hu, Z., Lu, X., Yao, Z. and Zhang, X., On curvature-adapted hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ and $\mathbb{H}^2\times \mathbb{H}^2$ , Internat. J. Math. 36(2) (2025), 22.Art. 245007Google Scholar
Hu, Z., Yao, Z. and Zhang, X., On Hopf hypersurfaces of the complex quadric with recurrent Ricci tensor, J. Geom. 112(3) (2021), 19.Art. 48.CrossRefGoogle Scholar
Hu, Z. and Zhang, X., On some hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ and $\mathbb{H}^2\times \mathbb{H}^2$ , Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 118(3) (2024), 16.Art. 116.Google Scholar
Li, H., Ma, H., Van der Veken, J., Vrancken, L. and Wang, X., Minimal Lagrangian submanifolds of the complex hyperquadric, Sci. China Math. 63(8) (2020), 1441–1462.CrossRefGoogle Scholar
Li, H., Vrancken, L., Wang, X. and Yao, Z., Hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ with constant sectional curvature, Calc. Var. Partial Differ. Equ. 63(7) (2024), 33.Art. 167.CrossRefGoogle Scholar
Li, H., Vrancken, L., Wang, X. and Yao, Z., Hypersurfaces of $\mathbb{H}^2\times \mathbb{H}^2$ with constant sectional curvature. Submitted.Google Scholar
Loo, T. H., Real hypersurfaces in a complex space form with recurrent Ricci tensor, Glasg. Math. J. 44(3) (2002), 547–550.CrossRefGoogle Scholar
Loo, T. H., Semi-parallel real hypersurfaces in complex two-plane Grassmannians, Differ. Geom. Appl. 34 (2014), 87–102.CrossRefGoogle Scholar
Lu, X., Wang, P. and Wang, X., On the geometry of hypersurfaces in $\mathbb{S}^2\times \mathbb{S}^2$ , Results Math. 7 (2023), 18. Art. 10.Google Scholar
Niebergall, R. and Ryan, P. J., Semi-parallel and semi-symmetric real hypersurfaces in complex space forms, Kyungpook Math. J. 38 (1998), 227–234.Google Scholar
Petersen, P., Riemannian geometry, Graduate texts in mathematics, vol. 171, 3rd edition, (Springer, Cham, 2016).Google Scholar
Torralbo, F. and Urbano, F., Surfaces with parallel mean curvature vector in $\mathbb{S}^2\times \mathbb{S}^2$ and $\mathbb{H}^2\times \mathbb{H}^2$ , Trans. Amer. Math. Soc. 364(2) (2012), 785–813.CrossRefGoogle Scholar
Torralbo, F. and Urbano, F., Minimal surfaces in $\mathbb{S}^2\times \mathbb{S}^2$ , J. Geom. Anal. 25(2) (2015), 1132–1156.CrossRefGoogle Scholar
Urbano, F., On hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ , Comm. Anal. Geom. 27(6) (2019), 1381–1416.CrossRefGoogle Scholar
Zhang, X., On Real Hypersurfaces in the (Nearly) Kähler Manifolds, PhD Thesis (Zhengzhou University, 2024).Google Scholar
Zhang, X., Gao, D., Hu, Z. and Yao, Z., On Hopf hypersurfaces of $\mathbb{S}^2\times \mathbb{S}^2$ and $\mathbb{H}^2\times \mathbb{H}^2$ , J. Geom. Phys. 194 (2023), 14.Art. 104996.Google Scholar