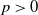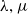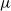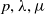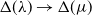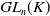1. Introduction
In the representation theory of the general linear group
![]() $GL_n(K)$
, where K is an infinite field of characteristic
$GL_n(K)$
, where K is an infinite field of characteristic
![]() $p>0$
, the Weyl modules
$p>0$
, the Weyl modules
![]() $\Delta(\lambda)$
are of central importance. These are parameterized by partitions
$\Delta(\lambda)$
are of central importance. These are parameterized by partitions
![]() $\lambda$
with at most n parts. Over a field of characteristic zero, the modules
$\lambda$
with at most n parts. Over a field of characteristic zero, the modules
![]() $\Delta(\lambda)$
are irreducible. However over fields of positive characteristics, this is no longer true and determining their structure is a major problem. In particular, very little is known about homomorphisms between them.
$\Delta(\lambda)$
are irreducible. However over fields of positive characteristics, this is no longer true and determining their structure is a major problem. In particular, very little is known about homomorphisms between them.
For
![]() $GL_3(K)$
, all homomorphisms between Weyl modules have been classified when
$GL_3(K)$
, all homomorphisms between Weyl modules have been classified when
![]() $p>2$
by Cox and Parker [Reference Cox and Parker5]. Some of the few general results are the nonvanishing theorems of Carter and Payne [Reference Carter and Payne4] and Koppinen [Reference Koppinen11], and the row or column removal theorems of Fayers and Lyle [Reference Lyle14] and Kulkarni [Reference Kulkarni12].
$p>2$
by Cox and Parker [Reference Cox and Parker5]. Some of the few general results are the nonvanishing theorems of Carter and Payne [Reference Carter and Payne4] and Koppinen [Reference Koppinen11], and the row or column removal theorems of Fayers and Lyle [Reference Lyle14] and Kulkarni [Reference Kulkarni12].
In [Reference Maliakas and Stergiopoulou17], we examined homomorphisms into hook Weyl modules and obtained a classification result. This has been obtained also by Loubert [Reference Loubert13] for
![]() $p>2$
. In the present paper, we consider homomorphisms
$p>2$
. In the present paper, we consider homomorphisms
![]() $\Delta(\lambda) \to \Delta(\mu)$
, where
$\Delta(\lambda) \to \Delta(\mu)$
, where
![]() $\mu$
has two parts. The main result, Theorem 3.1, provides sufficient arithmetic conditions on
$\mu$
has two parts. The main result, Theorem 3.1, provides sufficient arithmetic conditions on
![]() $\lambda, \mu$
, and p so that
$\lambda, \mu$
, and p so that
![]() $\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \neq 0$
, where S is the Schur algebra for
$\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \neq 0$
, where S is the Schur algebra for
![]() $GL_n(K)$
of appropriate degree. An explicit map is provided that corresponds to the sum of all standard tableaux of shape
$GL_n(K)$
of appropriate degree. An explicit map is provided that corresponds to the sum of all standard tableaux of shape
![]() $\mu$
and weight
$\mu$
and weight
![]() $\lambda$
. The main tool of the proof is the description of Weyl modules by generators and relations of Akin et al. [Reference Akin, Buchsbaum and Weyman2].
$\lambda$
. The main tool of the proof is the description of Weyl modules by generators and relations of Akin et al. [Reference Akin, Buchsbaum and Weyman2].
The first examples of pairs of Weyl modules with homomorphism spaces of dimension greater than 1 were obtained by Dodge [Reference Dodge6]. Shortly after, more were found by Lyle [Reference Lyle14]. In Corollary 6.2, we find sufficient conditions on
![]() $\lambda, \mu$
and p so that
$\lambda, \mu$
and p so that
![]() $\dim \textrm{Hom}_S(\Delta(\lambda), \Delta(\mu))>1$
and thus we have new examples of homomorphism spaces between Weyl modules of dimension greater than 1.
$\dim \textrm{Hom}_S(\Delta(\lambda), \Delta(\mu))>1$
and thus we have new examples of homomorphism spaces between Weyl modules of dimension greater than 1.
By a classical theorem of Carter and Lusztig [Reference Carter and Lusztig3], the results in Theorem 3.1 and Corollary 6.2 have analogues for Specht modules for the symmetric group when
![]() $p>2$
, see Remark 3.2 and the Remark after Corollary 6.2.
$p>2$
, see Remark 3.2 and the Remark after Corollary 6.2.
Section 2 is devoted to notation and preliminaries. In Section 3, we state the main result, and in Section 4, we consider the straightening law needed later. The proof of the main result is in Section 5. In Section 6, we consider homomorphism spaces of dimension greater than 1.
2. Preliminaries
2.1. Notation
Throughout this paper, K will be an infinite field of characteristic
![]() $p>0$
. We will be working with homogeneous polynomial representations of
$p>0$
. We will be working with homogeneous polynomial representations of
![]() $GL_n(K)$
of degree r, or equivalently, with modules over the Schur algebra
$GL_n(K)$
of degree r, or equivalently, with modules over the Schur algebra
![]() $S=S_K(n,r)$
. A standard reference here is [Reference Green8].
$S=S_K(n,r)$
. A standard reference here is [Reference Green8].
In what follows we fix notation and recall from Akin and Buchsbaum [Reference Akin and Buchsbaum1], and also Akin et al. [Reference Akin, Buchsbaum and Weyman2] important facts.
Let
![]() $V=K^n$
be the natural
$V=K^n$
be the natural
![]() $GL_n(K)$
-module. The divided power algebra
$GL_n(K)$
-module. The divided power algebra
![]() $DV=\sum_{i\geq 0}D_iV$
of V is defined as the graded dual of the Hopf algebra
$DV=\sum_{i\geq 0}D_iV$
of V is defined as the graded dual of the Hopf algebra
![]() $S(V^{*})$
, where
$S(V^{*})$
, where
![]() $V^{*}$
is the linear dual of V and
$V^{*}$
is the linear dual of V and
![]() $S(V^{*})$
is the symmetric algebra of
$S(V^{*})$
is the symmetric algebra of
![]() $V^{*}$
, see [Reference Akin, Buchsbaum and Weyman2], I.4. For
$V^{*}$
, see [Reference Akin, Buchsbaum and Weyman2], I.4. For
![]() $v \in V$
and i, j nonnegative integers, we will use many times relations of the form
$v \in V$
and i, j nonnegative integers, we will use many times relations of the form
where
![]() $\tbinom{i+j}{j}$
is the indicated binomial coefficient.
$\tbinom{i+j}{j}$
is the indicated binomial coefficient.
By
![]() $\wedge(n,r)$
, we denote the set of sequences
$\wedge(n,r)$
, we denote the set of sequences
![]() $a=(a_1, \dots, a_n)$
of nonnegative integers that sum to r and by
$a=(a_1, \dots, a_n)$
of nonnegative integers that sum to r and by
![]() $\wedge^+(n,r)$
we denote the subset of
$\wedge^+(n,r)$
we denote the subset of
![]() $\wedge(n,r)$
consisting of sequences
$\wedge(n,r)$
consisting of sequences
![]() $\lambda=(\lambda_1, \dots, \lambda_n)$
such that
$\lambda=(\lambda_1, \dots, \lambda_n)$
such that
![]() $\lambda_1 \ge \lambda_2 \dots \ge \lambda_n$
. Elements of
$\lambda_1 \ge \lambda_2 \dots \ge \lambda_n$
. Elements of
![]() $\wedge^+(n,r)$
are referred to as partitions of r with at most n parts. The transpose partition
$\wedge^+(n,r)$
are referred to as partitions of r with at most n parts. The transpose partition
![]() $\lambda^t =(\lambda_1^t,...,\lambda_q^t) \in \wedge^+(\lambda_1,r), q=\lambda_1,$
of a partition
$\lambda^t =(\lambda_1^t,...,\lambda_q^t) \in \wedge^+(\lambda_1,r), q=\lambda_1,$
of a partition
![]() $\lambda=(\lambda_1,...,\lambda_n) \in \wedge^+(n,r)$
is defined by
$\lambda=(\lambda_1,...,\lambda_n) \in \wedge^+(n,r)$
is defined by
![]() $\lambda_j^t = \# \{i\,{:}\, \lambda_i \ge j\}$
.
$\lambda_j^t = \# \{i\,{:}\, \lambda_i \ge j\}$
.
If
![]() $a=(a_1,\dots, a_n) \in \wedge(n,r)$
, we denote by D(a) or
$a=(a_1,\dots, a_n) \in \wedge(n,r)$
, we denote by D(a) or
![]() $D(a_1,\dots,a_n)$
the tensor product
$D(a_1,\dots,a_n)$
the tensor product
![]() $D_{a_1}V\otimes \dots \otimes D_{a_n}V$
. All tensor products in this paper are over K.
$D_{a_1}V\otimes \dots \otimes D_{a_n}V$
. All tensor products in this paper are over K.
The exterior algebra of V is denoted
![]() $\Lambda V=\sum_{i\geq 0}\Lambda^iV$
. If
$\Lambda V=\sum_{i\geq 0}\Lambda^iV$
. If
![]() $a=(a_1,\dots, a_n) \in \wedge(n,r)$
, we denote by
$a=(a_1,\dots, a_n) \in \wedge(n,r)$
, we denote by
![]() $\Lambda(a)$
the tensor product
$\Lambda(a)$
the tensor product
![]() $\Lambda^{a_1}V\otimes \dots \otimes \Lambda^{a_n}V$
.
$\Lambda^{a_1}V\otimes \dots \otimes \Lambda^{a_n}V$
.
For
![]() $\lambda \in \wedge^+(n,r)$
, we denote by
$\lambda \in \wedge^+(n,r)$
, we denote by
![]() $\Delta(\lambda)$
the corresponding Weyl module for S. In [Reference Akin, Buchsbaum and Weyman2], Definition II.1.4, the module
$\Delta(\lambda)$
the corresponding Weyl module for S. In [Reference Akin, Buchsbaum and Weyman2], Definition II.1.4, the module
![]() $\Delta(\lambda)$
(denoted
$\Delta(\lambda)$
(denoted
![]() $K_{\lambda}F$
there), was defined as the image a particular map
$K_{\lambda}F$
there), was defined as the image a particular map
![]() $d^{\prime}_{\lambda} \,{:}\, D(\lambda) \to \Lambda(\lambda^{t})$
. For example, if
$d^{\prime}_{\lambda} \,{:}\, D(\lambda) \to \Lambda(\lambda^{t})$
. For example, if
![]() $\lambda =(r)$
, then
$\lambda =(r)$
, then
![]() $\Delta(\lambda) =D_rV$
, and if
$\Delta(\lambda) =D_rV$
, and if
![]() $\lambda =(1^r)$
, then
$\lambda =(1^r)$
, then
![]() $\Delta(\lambda) =\Lambda^{r}V$
.
$\Delta(\lambda) =\Lambda^{r}V$
.
2.2. Relations for Weyl modules.
We recall from [Reference Akin, Buchsbaum and Weyman2], Theorem II.3.16, the following description of
![]() $\Delta (\lambda)$
in terms of generators and relations.
$\Delta (\lambda)$
in terms of generators and relations.
Theorem 2.1 ([Reference Akin, Buchsbaum and Weyman2]). Let
![]() $\lambda=(\lambda_1,\dots,\lambda_m) \in \wedge^+(n,r)$
, where
$\lambda=(\lambda_1,\dots,\lambda_m) \in \wedge^+(n,r)$
, where
![]() $\lambda_m >0$
. There is an exact sequence of S-modules
$\lambda_m >0$
. There is an exact sequence of S-modules
where the restriction of
![]() $ \square_{\lambda} $
to the summand
$ \square_{\lambda} $
to the summand
![]() $M_i(t)=D(\lambda_1,\dots,\lambda_i+t,\lambda_{i+1}-t,\dots,\lambda_m)$
is the composition
$M_i(t)=D(\lambda_1,\dots,\lambda_i+t,\lambda_{i+1}-t,\dots,\lambda_m)$
is the composition
where
![]() $\Delta\,{:}\,D(\lambda_i+t) \to D(\lambda_i,t)$
and
$\Delta\,{:}\,D(\lambda_i+t) \to D(\lambda_i,t)$
and
![]() $\eta\,{:}\,D(t,\lambda_{i+1}-t) \to D(\lambda_{i+1})$
are the indicated components of the comultiplication and multiplication, respectively, of the Hopf algebra DV and
$\eta\,{:}\,D(t,\lambda_{i+1}-t) \to D(\lambda_{i+1})$
are the indicated components of the comultiplication and multiplication, respectively, of the Hopf algebra DV and
![]() $d^{\prime}_\lambda$
is the map in [Reference Akin, Buchsbaum and Weyman2], Def.II.13.
$d^{\prime}_\lambda$
is the map in [Reference Akin, Buchsbaum and Weyman2], Def.II.13.
2.3. Standard basis of
 $\Delta(\mu)$
$\Delta(\mu)$
We will record here and in the next subsection two important facts from [Reference Akin, Buchsbaum and Weyman2] and [Reference Akin and Buchsbaum1] specified to the case of partitions consisting of two parts.
Let us fix the order
![]() $e_1<e_2<...<e_n$
on the set
$e_1<e_2<...<e_n$
on the set
![]() $\{e_1, e_2, ..., e_n\}$
of the canonical basis elements of the natural module V of
$\{e_1, e_2, ..., e_n\}$
of the canonical basis elements of the natural module V of
![]() $GL_n(K)$
. We will denote each element
$GL_n(K)$
. We will denote each element
![]() $e_i$
by its subscript i. For a partition
$e_i$
by its subscript i. For a partition
![]() $\mu=(\mu_1,\mu_2) \in \wedge^+(n,r)$
, a tableau of shape
$\mu=(\mu_1,\mu_2) \in \wedge^+(n,r)$
, a tableau of shape
![]() $\mu$
is a filling of the diagram of
$\mu$
is a filling of the diagram of
![]() $\mu$
with entries from
$\mu$
with entries from
![]() $\{1,...,n\}$
. Such a tableau is called standard if the entries are weakly increasing across the rows from left to right and strictly increasing in the columns from top to bottom. (The terminology used in [Reference Akin, Buchsbaum and Weyman2] is ’co-standard’).
$\{1,...,n\}$
. Such a tableau is called standard if the entries are weakly increasing across the rows from left to right and strictly increasing in the columns from top to bottom. (The terminology used in [Reference Akin, Buchsbaum and Weyman2] is ’co-standard’).
The set of standard tableaux of shape
![]() $\mu$
will be denoted by
$\mu$
will be denoted by
![]() $\textrm{ST}(\mu)$
. The weight of a tableau T is the tuple
$\textrm{ST}(\mu)$
. The weight of a tableau T is the tuple
![]() $\alpha=(\alpha_1,...,\alpha_n)$
, where
$\alpha=(\alpha_1,...,\alpha_n)$
, where
![]() $\alpha_i$
is the number of appearances of the entry i in T. The subset of
$\alpha_i$
is the number of appearances of the entry i in T. The subset of
![]() $\textrm{ST}(\mu)$
consisting of the (standard) tableaux of weight
$\textrm{ST}(\mu)$
consisting of the (standard) tableaux of weight
![]() $\alpha$
will be denoted by
$\alpha$
will be denoted by
![]() $\textrm{ST}_{\alpha}(\mu).$
$\textrm{ST}_{\alpha}(\mu).$
For example, the following tableau of shape
![]() $\mu=(6,4)$
.
$\mu=(6,4)$
.

is standard and has weight
![]() $\alpha=(3,4,1,2)$
.
$\alpha=(3,4,1,2)$
.
We will use ‘exponential’ notation for standard tableaux. Thus for the above example, we write
To each tableau T of shape
![]() $\mu=(\mu_1, \mu_2)$
, we may associate an element
$\mu=(\mu_1, \mu_2)$
, we may associate an element
where
![]() $x_T(i)=1^{(a_{i1})}\cdots n^{(a_{in})}$
and
$x_T(i)=1^{(a_{i1})}\cdots n^{(a_{in})}$
and
![]() $a_{ij}$
is equal to the number of appearances of j in the i-th row of T. For example, the T depicted above yields
$a_{ij}$
is equal to the number of appearances of j in the i-th row of T. For example, the T depicted above yields
![]() $x_T=1^{(3)}2^{(2)}4\otimes2^{(2)}34$
. According to [Reference Akin, Buchsbaum and Weyman2], Theorem II.2.16, we have the following.
$x_T=1^{(3)}2^{(2)}4\otimes2^{(2)}34$
. According to [Reference Akin, Buchsbaum and Weyman2], Theorem II.2.16, we have the following.
Theorem 2.2 ([Reference Akin, Buchsbaum and Weyman2]). The set
![]() $\{d^{\prime}_{\mu}(x_T)\,{:}\, T \in \textrm{ST}(\mu)\}$
is a basis of the K-vector space
$\{d^{\prime}_{\mu}(x_T)\,{:}\, T \in \textrm{ST}(\mu)\}$
is a basis of the K-vector space
![]() $\Delta({\mu})$
.
$\Delta({\mu})$
.
If
![]() $x=1^{(a_1)}2^{(a_2)}\cdots n^{(a_n)} \otimes 1^{(b_1)}2^{(b_2)}\cdots n^{(b_n)} \in D(\mu)$
, we will denote the element
$x=1^{(a_1)}2^{(a_2)}\cdots n^{(a_n)} \otimes 1^{(b_1)}2^{(b_2)}\cdots n^{(b_n)} \in D(\mu)$
, we will denote the element
![]() $d^{\prime}_{\mu}(x) \in \Delta(\mu)$
by
$d^{\prime}_{\mu}(x) \in \Delta(\mu)$
by
 \[ \left[\begin{array}{l} 1^{(a_1)} 2^{(a_2)} \cdots n^{(a_n)} \\ \\[-8pt] 1^{(b_1)} 2^{(a_2)} \cdots n^{(b_n)} \end{array}\right]. \]
\[ \left[\begin{array}{l} 1^{(a_1)} 2^{(a_2)} \cdots n^{(a_n)} \\ \\[-8pt] 1^{(b_1)} 2^{(a_2)} \cdots n^{(b_n)} \end{array}\right]. \]
2.4. Weight subspaces of
 $\Delta(\mu)$
$\Delta(\mu)$
Suppose
![]() $n \ge r$
. Let
$n \ge r$
. Let
![]() $\nu \in \wedge(n,r)$
and
$\nu \in \wedge(n,r)$
and
![]() $\mu=(\mu_1,\mu_2) \in \wedge^+(2,r)$
. According to [Reference Akin and Buchsbaum1], equation (11), a basis of the K-vector space
$\mu=(\mu_1,\mu_2) \in \wedge^+(2,r)$
. According to [Reference Akin and Buchsbaum1], equation (11), a basis of the K-vector space
![]() $\textrm{Hom}_S(D(\nu), \Delta(\mu))$
is in 1-1 correspondence with set
$\textrm{Hom}_S(D(\nu), \Delta(\mu))$
is in 1-1 correspondence with set
![]() $\textrm{ST}_{\nu}(\mu)$
of standard tableaux of shape
$\textrm{ST}_{\nu}(\mu)$
of standard tableaux of shape
![]() $\mu$
and weight
$\mu$
and weight
![]() $\nu$
.
$\nu$
.
For the computations to follow, we need to make the above correspondence explicit. Let
![]() $\nu = (\nu_1,..., \nu_n) \in \wedge(n,r)$
and
$\nu = (\nu_1,..., \nu_n) \in \wedge(n,r)$
and
![]() $T \in \textrm{ST}_{\nu}(\mu)$
. Let
$T \in \textrm{ST}_{\nu}(\mu)$
. Let
![]() $a_i$
(respectively,
$a_i$
(respectively,
![]() $b_i$
) be the number of appearances of i in the first row (respectively, second row) of T. We note that
$b_i$
) be the number of appearances of i in the first row (respectively, second row) of T. We note that
![]() $\nu_i = a_i+b_i$
for each i. In particular, we have
$\nu_i = a_i+b_i$
for each i. In particular, we have
![]() $a_1 = \nu_1$
because of standardness of T. Define the map
$a_1 = \nu_1$
because of standardness of T. Define the map
where
![]() $\sum_{i_s}x_{si_s}(a_s) \otimes x_{si_s}(b_s)'$
is the image of
$\sum_{i_s}x_{si_s}(a_s) \otimes x_{si_s}(b_s)'$
is the image of
![]() $x_s$
under the component
$x_s$
under the component
of the diagonalization
![]() $\Delta \,{:}\, DV \to DV \otimes DV$
of the Hopf algebra DV for
$\Delta \,{:}\, DV \to DV \otimes DV$
of the Hopf algebra DV for
![]() $s=2,...,n$
. Thus we have that a basis of the K-vector space
$s=2,...,n$
. Thus we have that a basis of the K-vector space
![]() $\textrm{Hom}_S(D(\nu), \Delta(\mu))$
is the set
$\textrm{Hom}_S(D(\nu), \Delta(\mu))$
is the set
In particular, suppose
![]() $\lambda=(\lambda_1,...,\lambda_m) \in \wedge^+(n,r)$
is a partition and
$\lambda=(\lambda_1,...,\lambda_m) \in \wedge^+(n,r)$
is a partition and
![]() $\mu =(\mu_1,\mu_2) \in \wedge^+(2,r)$
satisfies
$\mu =(\mu_1,\mu_2) \in \wedge^+(2,r)$
satisfies
![]() $\mu_2 \le \lambda_1$
. This inequality means that each tableau of shape
$\mu_2 \le \lambda_1$
. This inequality means that each tableau of shape
![]() $\mu$
that has the form
$\mu$
that has the form
is standard. Hence, we have the following result.
Lemma 2.3. Suppose
![]() $n \ge r$
. Let
$n \ge r$
. Let
![]() $\lambda,\mu \in \wedge^{+}(n,r)$
, where
$\lambda,\mu \in \wedge^{+}(n,r)$
, where
![]() $\lambda=(\lambda_1,...,\lambda_m)$
and
$\lambda=(\lambda_1,...,\lambda_m)$
and
![]() $ \mu=(\mu_1, \mu_2)$
. If
$ \mu=(\mu_1, \mu_2)$
. If
![]() $\mu_2 \le \lambda_1$
, than a basis of the K- vector space
$\mu_2 \le \lambda_1$
, than a basis of the K- vector space
![]() $\textrm{Hom}_S(D(\lambda), \Delta(\mu))$
is given by the elements
$\textrm{Hom}_S(D(\lambda), \Delta(\mu))$
is given by the elements
![]() $\phi_T$
, where
$\phi_T$
, where
are such that
Example. Suppose
![]() $\lambda=(\lambda_1,3,3)$
and
$\lambda=(\lambda_1,3,3)$
and
![]() $\mu=(\lambda_1+4,2)$
, where
$\mu=(\lambda_1+4,2)$
, where
![]() $\lambda_1 \ge 3$
. Then
$\lambda_1 \ge 3$
. Then
![]() $\{[T_1],[T_2],[T_3]\}$
is a basis of
$\{[T_1],[T_2],[T_3]\}$
is a basis of
![]() $\textrm{Hom}_S(D(\lambda), \Delta(\mu))$
, where
$\textrm{Hom}_S(D(\lambda), \Delta(\mu))$
, where
For
![]() $x=1^{(\lambda_1)} \otimes 1^{(2)}2 \otimes 3^{(3)} \in D(\lambda)$
and
$x=1^{(\lambda_1)} \otimes 1^{(2)}2 \otimes 3^{(3)} \in D(\lambda)$
and
![]() $T=T_2$
, we have
$T=T_2$
, we have
 \[\phi_T(x)=\binom{\lambda_1+2}{2}\left[\begin{array}{l} 1^{(\lambda_1+2)} 3^{(2)} \\ \\[-9pt] 23\end{array}\right]+\binom{\lambda_1+1}{1}\left[\begin{array}{l} 1^{(\lambda_1+1)} 23^{(2)} \\ \\[-9pt] 13\end{array}\right],\]
\[\phi_T(x)=\binom{\lambda_1+2}{2}\left[\begin{array}{l} 1^{(\lambda_1+2)} 3^{(2)} \\ \\[-9pt] 23\end{array}\right]+\binom{\lambda_1+1}{1}\left[\begin{array}{l} 1^{(\lambda_1+1)} 23^{(2)} \\ \\[-9pt] 13\end{array}\right],\]
where the binomial coefficients come from multiplication in the divided power algebra DV.
3. Main result
In order to state the main result of this paper, we use the following notation. If x, y are positive integers, let
If x is a positive integer, let
![]() $R(x,0)=0$
.
$R(x,0)=0$
.
Theorem 3.1. Let K be an infinite field of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $n \ge r$
be positive integers. Let
$n \ge r$
be positive integers. Let
![]() $\lambda,\mu \in \wedge^{+}(n,r)$
be partitions such that
$\lambda,\mu \in \wedge^{+}(n,r)$
be partitions such that
![]() $\lambda=(\lambda_1,...,\lambda_m)$
and
$\lambda=(\lambda_1,...,\lambda_m)$
and
![]() $\mu =(\mu_1, \mu_2)$
, where
$\mu =(\mu_1, \mu_2)$
, where
![]() $\lambda_m \neq 0$
,
$\lambda_m \neq 0$
,
![]() $m \ge 2$
and
$m \ge 2$
and
![]() $\mu_2 \le \lambda_1 \le \mu_1$
. If p divides all of the following integers
$\mu_2 \le \lambda_1 \le \mu_1$
. If p divides all of the following integers
then the map
induces a nonzero homomorphism
![]() $\Delta(\lambda) \to \Delta(\mu).$
$\Delta(\lambda) \to \Delta(\mu).$
Remark 3.2. Consider the symmetric group
![]() $\mathfrak{S}_r$
on r symbols. For a partition
$\mathfrak{S}_r$
on r symbols. For a partition
![]() $\lambda$
of r, let
$\lambda$
of r, let
![]() $\textrm{Sp}(\lambda)$
be the corresponding Specht module defined in Section 6.3 of [Reference Green8]. From Theorem 3.7 of [Reference Carter and Lusztig3], we have
$\textrm{Sp}(\lambda)$
be the corresponding Specht module defined in Section 6.3 of [Reference Green8]. From Theorem 3.7 of [Reference Carter and Lusztig3], we have
for all partitions
![]() $\lambda, \mu$
of r. (In fact we have equality if
$\lambda, \mu$
of r. (In fact we have equality if
![]() $p>2$
according to loc. cit.) Hence, our Theorem 3.1 may be considered as a nonvanishing result for homomorphisms between Specht modules.
$p>2$
according to loc. cit.) Hence, our Theorem 3.1 may be considered as a nonvanishing result for homomorphisms between Specht modules.
Remark 3.3. Here we make some comments concerning the inequalities
![]() $n \ge r$
,
$n \ge r$
,
![]() $m \ge 2$
and
$m \ge 2$
and
![]() $\mu_2 \le \lambda_1 \le \mu_1$
in the statement of the above theorem.
$\mu_2 \le \lambda_1 \le \mu_1$
in the statement of the above theorem.
-
(1) The assumption
 $n \ge r$
is needed so that the Weyl modules
$n \ge r$
is needed so that the Weyl modules
 $\Delta(\lambda), \Delta(\mu)$
are nonzero. As is usual with such results, it turns out that this assumption may be relaxed to
$\Delta(\lambda), \Delta(\mu)$
are nonzero. As is usual with such results, it turns out that this assumption may be relaxed to
 $n \ge m$
, since m is the maximum number of parts of the partitions
$n \ge m$
, since m is the maximum number of parts of the partitions
 $\lambda, \mu$
. This follows from the proof of the theorem to be given in Section 5.
$\lambda, \mu$
. This follows from the proof of the theorem to be given in Section 5. -
It is well known that if
 $\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \neq 0,$
then
$\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \neq 0,$
then
 $\lambda \trianglelefteq \mu$
in the dominance ordering, meaning in particular that
$\lambda \trianglelefteq \mu$
in the dominance ordering, meaning in particular that
 $\lambda_1\le \mu_1$
.
$\lambda_1\le \mu_1$
. -
If
 $m=1$
, then by the previous remark,
$m=1$
, then by the previous remark,
 $\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) = 0$
, unless
$\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) = 0$
, unless
 $\mu = \lambda $
, in which case
$\mu = \lambda $
, in which case
 $\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) =K$
by [Reference Jantzen10], the analogue for Weyl modules of II.2.8 Proposition.
$\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) =K$
by [Reference Jantzen10], the analogue for Weyl modules of II.2.8 Proposition. -
(2) In the above remarks, the corresponding inequalities were needed to avoid trivial situations. The nature of the assumption
 $\mu_2 \le \lambda_1$
is different. There are cases where nonzero homomorphisms
$\mu_2 \le \lambda_1$
is different. There are cases where nonzero homomorphisms
 $\Delta(\lambda) \to \Delta(\mu)$
exist if
$\Delta(\lambda) \to \Delta(\mu)$
exist if
 $\mu_2>\lambda_1$
. For example, let
$\mu_2>\lambda_1$
. For example, let
 $n=3$
,
$n=3$
,
 $p=2$
,
$p=2$
,
 $\lambda=(2,2,2)$
and
$\lambda=(2,2,2)$
and
 $\mu=(3,3)$
. One may check that the map
$\mu=(3,3)$
. One may check that the map
 $\phi_T$
, where
$\phi_T$
, where
 $T= \begin{array}{l} 1^{(2)} 2\\ 2 3^{(2)}\end{array},$
induces a nonzero map
$T= \begin{array}{l} 1^{(2)} 2\\ 2 3^{(2)}\end{array},$
induces a nonzero map
 $\Delta(\lambda) \to \Delta(\mu)$
. It would be interesting to find general results.
$\Delta(\lambda) \to \Delta(\mu)$
. It would be interesting to find general results. -
The main point for us of the assumption
 $\mu_2 \le \lambda_1$
is that every tableau T in Lemma 2.3 is standard.
$\mu_2 \le \lambda_1$
is that every tableau T in Lemma 2.3 is standard. -
(3) If
 $\lambda_1=\mu_1$
, then
$\lambda_1=\mu_1$
, then
 $R(\lambda_1-\mu_2+1,l)=0$
and the first divisibility condition of the theorem holds for all p. The remaining divisibility conditions are exactly those for which we have
$R(\lambda_1-\mu_2+1,l)=0$
and the first divisibility condition of the theorem holds for all p. The remaining divisibility conditions are exactly those for which we have
 $\textrm{Hom}_{S'}(\Delta(\lambda_2,...,\lambda_m),\Delta(\mu_2)) \neq 0,$
where
$\textrm{Hom}_{S'}(\Delta(\lambda_2,...,\lambda_m),\Delta(\mu_2)) \neq 0,$
where
 $S'=S_K(n,r-\lambda_1)$
. This follows, for example, from Theorem 3.1 of [Reference Maliakas and Stergiopoulou17]. Hence, in this case, we have an instance of row removal which states that
$S'=S_K(n,r-\lambda_1)$
. This follows, for example, from Theorem 3.1 of [Reference Maliakas and Stergiopoulou17]. Hence, in this case, we have an instance of row removal which states that
 $\dim \textrm{Hom}_S(\Delta(\lambda),\Delta(\mu)) = \dim \textrm{Hom}_{S'}(\Delta(\lambda_2,...,\lambda_m),\Delta(\mu_2))$
. See the paper by Fayers and Lyle [Reference Fayers and Lyle7], Theorem 2.2 (stated for Specht modules), or the paper by Kulkarni [Reference Kulkarni12], Proposition 1.2.
$\dim \textrm{Hom}_S(\Delta(\lambda),\Delta(\mu)) = \dim \textrm{Hom}_{S'}(\Delta(\lambda_2,...,\lambda_m),\Delta(\mu_2))$
. See the paper by Fayers and Lyle [Reference Fayers and Lyle7], Theorem 2.2 (stated for Specht modules), or the paper by Kulkarni [Reference Kulkarni12], Proposition 1.2.
For further use, we note that the divisibility assumptions of Theorem 3.1 may be stated in a different way. For a positive integer y, let
![]() $l_{p}(y)$
be the least integer i such that
$l_{p}(y)$
be the least integer i such that
![]() $p^i>y$
. From James [Reference James9], Corollary 22.5, we have the following result.
$p^i>y$
. From James [Reference James9], Corollary 22.5, we have the following result.
Lemma 3.4 ([Reference James9]). Let
![]() $x \ge y$
be positive integers. Then p divides R(x, y) if and only if
$x \ge y$
be positive integers. Then p divides R(x, y) if and only if
![]() $p^{l_{p}(y)} $
divides x.
$p^{l_{p}(y)} $
divides x.
4. Straightening
For the proof of Theorem 3.1, we will need the following identities involving binomial coefficients. Our convention is that
![]() $\tbinom{a}{b}=0$
if
$\tbinom{a}{b}=0$
if
![]() $b>a$
or
$b>a$
or
![]() $b<0$
.
$b<0$
.
Lemma 4.1.
-
(1) Let
 $a, m_1, ..., m_s$
be nonnegative integers and
$a, m_1, ..., m_s$
be nonnegative integers and
 $m=m_1+\cdots+m_s$
.
$m=m_1+\cdots+m_s$
. -
a. We have
where the sum ranges over all nonnegative integers \[\sum_{j_1+\cdots+j_s = a}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}=\binom{m}{a},\]
\[\sum_{j_1+\cdots+j_s = a}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}=\binom{m}{a},\]
 $j_1,...,j_s$
such that
$j_1,...,j_s$
such that
 $j_1+\cdots+j_s = a.$
$j_1+\cdots+j_s = a.$
-
b. If
 $m>0$
, then where the sum ranges over all nonnegative integers
$m>0$
, then where the sum ranges over all nonnegative integers \[\sum_{j_0+\cdots+j_s = m}(\!-1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}=0,\]
\[\sum_{j_0+\cdots+j_s = m}(\!-1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}=0,\]
 $j_0,...,j_s$
such that
$j_0,...,j_s$
such that
 $j_0+\cdots+j_s = m.$
$j_0+\cdots+j_s = m.$
-
(2) Let a, b, c be nonnegative integers such that
 $ b \le a$
. Then
$ b \le a$
. Then  \begin{align*}&\sum_{j=0}^{c}(\!-1)^{c-j}\binom{a+j}{j}\binom{b}{c-j}=\binom{a-b+c}{c}= \sum_{j=0}^{c}(\!-1)^{\,j}\binom{a+c-j}{c-j}\binom{b}{j}.\end{align*}
\begin{align*}&\sum_{j=0}^{c}(\!-1)^{c-j}\binom{a+j}{j}\binom{b}{c-j}=\binom{a-b+c}{c}= \sum_{j=0}^{c}(\!-1)^{\,j}\binom{a+c-j}{c-j}\binom{b}{j}.\end{align*}
Proof.
-
(1) The identity in (a) is Vandermonde’s identity. For (b), we have
 \begin{align*} \sum_{j_0+\cdots+j_s = m}(\!-1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}&= \sum_{j_0=0}^{m} \; \sum_{j_1+\cdots+j_s = m-j_0}(-\!1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}\\& =\sum_{j_0=0}^{m} (\!-1)^{j_0}\sum_{j_1+\cdots+j_s = m-j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}\\&= \sum_{j_0=0}^{m} (\!-1)^{j_0}\binom{m}{m-j_0}\\&= 0. \end{align*}
\begin{align*} \sum_{j_0+\cdots+j_s = m}(\!-1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}&= \sum_{j_0=0}^{m} \; \sum_{j_1+\cdots+j_s = m-j_0}(-\!1)^{j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}\\& =\sum_{j_0=0}^{m} (\!-1)^{j_0}\sum_{j_1+\cdots+j_s = m-j_0}\binom{m_1}{ j_1}\cdots \binom{m_s}{j_s}\\&= \sum_{j_0=0}^{m} (\!-1)^{j_0}\binom{m}{m-j_0}\\&= 0. \end{align*}
-
(2) The second identity is Lemma 2.6 of [Reference Lyle14] for
 $q=1$
. The first follows from the second with the substitution
$q=1$
. The first follows from the second with the substitution
 $ j \mapsto c-j$
.
$ j \mapsto c-j$
.
We will also need the following explicit form of the straightening law concerning violations of standardness in the first column.
Lemma 4.2. Let
![]() $\mu=(\mu_1, \mu_2) \in \wedge^+(n,r)$
,
$\mu=(\mu_1, \mu_2) \in \wedge^+(n,r)$
,
![]() $(a_1,...,a_n) \in \wedge (n, \mu_1)$
and
$(a_1,...,a_n) \in \wedge (n, \mu_1)$
and
![]() $(b_1,...,b_n) \in \wedge (n, \mu_2)$
.
$(b_1,...,b_n) \in \wedge (n, \mu_2)$
.
-
(1) If
 $a_1+b_1 > \mu_1$
, then
$a_1+b_1 > \mu_1$
, then
 $\left[\begin{array}{l} 1^{(a_1)} \cdots n^{(a_n)} \\ 1^{(b_1)} \cdots n^{(b_n)} \end{array}\right]=0$
.
$\left[\begin{array}{l} 1^{(a_1)} \cdots n^{(a_n)} \\ 1^{(b_1)} \cdots n^{(b_n)} \end{array}\right]=0$
. -
(2) If
 $a_1+b_1 \le \mu_1$
, then in
$a_1+b_1 \le \mu_1$
, then in
 $\Delta (\mu)$
we have where the sum ranges over all nonnegative integers
$\Delta (\mu)$
we have where the sum ranges over all nonnegative integers \begin{equation*} \left[\begin{array}{l} 1^{(a_1)} \cdots n^{(a_n)} \\ 1^{(b_1)} \cdots n^{(b_n)} \end{array}\right]=(\!-1)^{b_1}\sum_{i_2,...,i_n} \binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-i_2)} \cdots n^{(a_n-i_n)} \\ 2^{(b_2+i_2)} \cdots n^{(b_n+i_n)} \end{array}\right],\end{equation*}
\begin{equation*} \left[\begin{array}{l} 1^{(a_1)} \cdots n^{(a_n)} \\ 1^{(b_1)} \cdots n^{(b_n)} \end{array}\right]=(\!-1)^{b_1}\sum_{i_2,...,i_n} \binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-i_2)} \cdots n^{(a_n-i_n)} \\ 2^{(b_2+i_2)} \cdots n^{(b_n+i_n)} \end{array}\right],\end{equation*}
 $i_2, ..., i_n$
such that
$i_2, ..., i_n$
such that
 $i_2+\cdots+i_n=b_1$
and
$i_2+\cdots+i_n=b_1$
and
 $i_s \le a_s$
for all
$i_s \le a_s$
for all
 $s=2,...,n$
.
$s=2,...,n$
.
Proof.
-
(1) This is clear since there is no element in
 $\Delta(\mu)$
of weight
$\Delta(\mu)$
of weight
 $(\nu_1,...,\nu_n)$
satisfying
$(\nu_1,...,\nu_n)$
satisfying
 $\nu_1 > \mu_1$
.
$\nu_1 > \mu_1$
. -
(2) We proceed by induction on
 $b_1$
, the case
$b_1$
, the case
 $b_1=0$
being clear. Suppose
$b_1=0$
being clear. Suppose
 $b_1>0$
. Consider the element
$b_1>0$
. Consider the element
 $x \in D(\mu_1+b_1, \mu_2-b_1)$
, where and the map
$x \in D(\mu_1+b_1, \mu_2-b_1)$
, where and the map \[x=1^{(a_1+b_1)}2^{(a_2)}\cdots n^{(a_n)} \otimes 2^{(b_2)}\cdots n^{(b_n)},\]
According to the analogue of Lemma II.2.9 of [Reference Akin, Buchsbaum and Weyman2] for divided powers in place of exterior powers, we have
\[x=1^{(a_1+b_1)}2^{(a_2)}\cdots n^{(a_n)} \otimes 2^{(b_2)}\cdots n^{(b_n)},\]
According to the analogue of Lemma II.2.9 of [Reference Akin, Buchsbaum and Weyman2] for divided powers in place of exterior powers, we have \begin{align*} \delta \,{:}\, D(\mu_1+b_1, \mu_2-b_1) \xrightarrow{\Delta \otimes 1} D(\mu_1, b_1, \mu_2-b_1) \xrightarrow{1 \otimes \eta } D(\mu_1, \mu_2). \end{align*}
\begin{align*} \delta \,{:}\, D(\mu_1+b_1, \mu_2-b_1) \xrightarrow{\Delta \otimes 1} D(\mu_1, b_1, \mu_2-b_1) \xrightarrow{1 \otimes \eta } D(\mu_1, \mu_2). \end{align*}
 $d^{\prime}_{\mu}(\delta(x))=0$
in
$d^{\prime}_{\mu}(\delta(x))=0$
in
 $\Delta(\mu_1,\mu_2)$
. Thus
$\Delta(\mu_1,\mu_2)$
. Thus
where the sum ranges over all nonnegative integers
![]() $j_1, ..., j_n$
such that
$j_1, ..., j_n$
such that
![]() $j_1+\cdots+j_n=b_1$
,
$j_1+\cdots+j_n=b_1$
,
![]() $j_1<b_1$
and
$j_1<b_1$
and
![]() $j_s \le a_s$
for all
$j_s \le a_s$
for all
![]() $s=2,...,n$
. Let X be the right hand side of the above equality. By induction, we have
$s=2,...,n$
. Let X be the right hand side of the above equality. By induction, we have
 \begin{align*} X=-\sum_{j_1,...,j_n} \binom{b_2+j_2}{b_2} \cdots \binom{b_n+j_n}{b_n}(\!-1)^{j_1}\sum_{k_2,...,k_n} \binom{b_2+j_2+k_2}{b_2+j_2} \cdots \binom{b_n+j_n+k_n}{b_n+j_n} \\ \left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-j_2-k_2)} \cdots n^{(a_n-j_n-k_n)} \\ 2^{(b_2+j_2+k_2)} \cdots n^{(b_n+j_n+k_n)} \end{array}\right], \end{align*}
\begin{align*} X=-\sum_{j_1,...,j_n} \binom{b_2+j_2}{b_2} \cdots \binom{b_n+j_n}{b_n}(\!-1)^{j_1}\sum_{k_2,...,k_n} \binom{b_2+j_2+k_2}{b_2+j_2} \cdots \binom{b_n+j_n+k_n}{b_n+j_n} \\ \left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-j_2-k_2)} \cdots n^{(a_n-j_n-k_n)} \\ 2^{(b_2+j_2+k_2)} \cdots n^{(b_n+j_n+k_n)} \end{array}\right], \end{align*}
where the new sum ranges over all nonnegative integers
![]() $k_2, ..., k_n$
such that
$k_2, ..., k_n$
such that
![]() $k_2+\cdots+k_n=j_1$
and
$k_2+\cdots+k_n=j_1$
and
![]() $k_s \le a_s-j_s$
for all
$k_s \le a_s-j_s$
for all
![]() $s=2,...,n$
. Using the identities
$s=2,...,n$
. Using the identities
for
![]() $s=2,...,n$
, we obtain
$s=2,...,n$
, we obtain
 \begin{align*} X=-\sum_{j_1,...,j_n,k_2,...,k_n}(\!-1)^{j_1} \binom{b_2+j_2+k_2}{b_2} \cdots \binom{b_n+j_n+k_n}{b_n}\binom{j_2+k_2}{j_2} \cdots \binom{j_n+k_n}{j_n} \\ \left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-j_2-k_2)} \cdots n^{(a_n-j_n-k_n)} \\ 2^{(b_2+j_2+k_2)} \cdots n^{(b_n+j_n+k_n)} \end{array}\right]. \end{align*}
\begin{align*} X=-\sum_{j_1,...,j_n,k_2,...,k_n}(\!-1)^{j_1} \binom{b_2+j_2+k_2}{b_2} \cdots \binom{b_n+j_n+k_n}{b_n}\binom{j_2+k_2}{j_2} \cdots \binom{j_n+k_n}{j_n} \\ \left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-j_2-k_2)} \cdots n^{(a_n-j_n-k_n)} \\ 2^{(b_2+j_2+k_2)} \cdots n^{(b_n+j_n+k_n)} \end{array}\right]. \end{align*}
The coefficient c of
 \[\left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-i_2)} \cdots n^{(a_n-i_n)} \\ \\[-8pt] 2^{(b_2+i_2)} \cdots n^{(b_n+i_n)} \end{array}\right] \]
\[\left[\begin{array}{l} 1^{(a_1+b_1)} 2^{(a_2-i_2)} \cdots n^{(a_n-i_n)} \\ \\[-8pt] 2^{(b_2+i_2)} \cdots n^{(b_n+i_n)} \end{array}\right] \]
in the right hand side of the above equation is equal to
 \[-\sum_{\substack{j_1,...,j_n,k_2,...,k_n \\ j_s+k_s=i_s}}(\!-1)^{j_1} \binom{b_2+j_2+k_2}{b_2} \cdots \binom{b_n+j_n+k_n}{b_n}\binom{j_2+k_2}{j_2} \cdots \binom{j_n+k_n}{j_n},\]
\[-\sum_{\substack{j_1,...,j_n,k_2,...,k_n \\ j_s+k_s=i_s}}(\!-1)^{j_1} \binom{b_2+j_2+k_2}{b_2} \cdots \binom{b_n+j_n+k_n}{b_n}\binom{j_2+k_2}{j_2} \cdots \binom{j_n+k_n}{j_n},\]
where the sum is restricted over those
![]() $j_1,...,j_n$
and
$j_1,...,j_n$
and
![]() $k_2,...,k_n$
that satisfy the additional conditions
$k_2,...,k_n$
that satisfy the additional conditions
![]() $j_s+k_s=i_s$
for all
$j_s+k_s=i_s$
for all
![]() $s=2,...,n.$
Hence
$s=2,...,n.$
Hence
 \begin{align*}c&=-\sum_{j_1,...,j_n}(\!-1)^{j_1} \binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\binom{i_2}{j_2} \cdots \binom{i_n}{j_n} \\& =-\binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\sum_{j_1,...,j_n}(\!-1)^{j_1} \binom{i_2}{j_2} \cdots \binom{i_n}{j_n}.\\& \end{align*}
\begin{align*}c&=-\sum_{j_1,...,j_n}(\!-1)^{j_1} \binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\binom{i_2}{j_2} \cdots \binom{i_n}{j_n} \\& =-\binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}\sum_{j_1,...,j_n}(\!-1)^{j_1} \binom{i_2}{j_2} \cdots \binom{i_n}{j_n}.\\& \end{align*}
Remembering that in the last sum we have
![]() $j_1<b_1$
, Lemma 4.1 (1)(b) yields
$j_1<b_1$
, Lemma 4.1 (1)(b) yields
Thus
![]() $c=(\!-1)^{b_1}\binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}.$
$c=(\!-1)^{b_1}\binom{b_2+i_2}{b_2} \cdots \binom{b_n+i_n}{b_n}.$
5. Proof of the main theorem
Consider the map
![]() $\psi \in \textrm{Hom}_S(D(\lambda), \Delta(\mu))$
given by the sum
$\psi \in \textrm{Hom}_S(D(\lambda), \Delta(\mu))$
given by the sum
in the statement of Theorem 3.1 We will show, according to Theorem 2.1, that
![]() $\psi(x)=0$
for every
$\psi(x)=0$
for every
![]() $x \in Im(\square_\lambda)$
. First we look at the relations corresponding to rows 1 and 2 of
$x \in Im(\square_\lambda)$
. First we look at the relations corresponding to rows 1 and 2 of
![]() $\Delta(\lambda)$
.
$\Delta(\lambda)$
.
Relations from rows 1 and 2
Let
![]() $x=1^{(\lambda_1)}\otimes 1^{(t)}2^{(\lambda_2-t)}\otimes3^{(\lambda_3)}\cdots m^{(\lambda_m)} \in Im(\square_\lambda),$
where
$x=1^{(\lambda_1)}\otimes 1^{(t)}2^{(\lambda_2-t)}\otimes3^{(\lambda_3)}\cdots m^{(\lambda_m)} \in Im(\square_\lambda),$
where
![]() $t\le \lambda_2$
, and let
$t\le \lambda_2$
, and let
![]() $T \in \textrm{ST}_{\lambda}(\mu).$
Then T is of the form
$T \in \textrm{ST}_{\lambda}(\mu).$
Then T is of the form
where the
![]() $a_i, b_i$
satisfy the conditions of Lemma 2.3. Using the definition of
$a_i, b_i$
satisfy the conditions of Lemma 2.3. Using the definition of
![]() $\phi_T$
from 2.4, we have
$\phi_T$
from 2.4, we have
If
![]() $(\lambda_1+i)+(t-i) \ge \mu_1$
, then by the first part of Lemma 4.2 we obtain
$(\lambda_1+i)+(t-i) \ge \mu_1$
, then by the first part of Lemma 4.2 we obtain
![]() $\phi_T(x)=0$
. Hence we may assume that
$\phi_T(x)=0$
. Hence we may assume that
![]() $t \le min\{\lambda_2, \mu_1-\lambda_1\}. $
Using the second part of Lemma 4.2, we have
$t \le min\{\lambda_2, \mu_1-\lambda_1\}. $
Using the second part of Lemma 4.2, we have
 \begin{align*}\phi_T(x)=& \sum_{i\le t}\binom{\lambda_1+i}{i}(\!-1)^{t-i} \sum_{k_2+\cdots+k_m=t-i}\binom{b_2-k_3-\cdots-k_m}{k_2}\binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&\qquad \left[\begin{array}{l} 1^{(\lambda_1+t)}2^{(a_2+k_3+\cdots+k_m)}3^{(a_3-k_3)} \cdots m^{(a_m-k_m)} \\ 2^{(b_2-k_3-\cdots-k_m)}3^{(b_3+k_3)} \cdots m^{(b_m+k_m)} \end{array}\right].\end{align*}
\begin{align*}\phi_T(x)=& \sum_{i\le t}\binom{\lambda_1+i}{i}(\!-1)^{t-i} \sum_{k_2+\cdots+k_m=t-i}\binom{b_2-k_3-\cdots-k_m}{k_2}\binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&\qquad \left[\begin{array}{l} 1^{(\lambda_1+t)}2^{(a_2+k_3+\cdots+k_m)}3^{(a_3-k_3)} \cdots m^{(a_m-k_m)} \\ 2^{(b_2-k_3-\cdots-k_m)}3^{(b_3+k_3)} \cdots m^{(b_m+k_m)} \end{array}\right].\end{align*}
Let
![]() $c \in K$
be the coefficient of
$c \in K$
be the coefficient of
![]() $\left[\begin{array}{l} 1^{(\lambda_1+t)}2^{(a_2+k_3+\cdots+k_m)}3^{(a_3-k_3)} \cdots m^{(a_m-k_m)} \\ 2^{(b_2-k_3-\cdots-k_m)}3^{(b_3+k_3)} \cdots m^{(b_m+k_m)}\end{array}\right] $
in the right hand side of the last equation and let
$\left[\begin{array}{l} 1^{(\lambda_1+t)}2^{(a_2+k_3+\cdots+k_m)}3^{(a_3-k_3)} \cdots m^{(a_m-k_m)} \\ 2^{(b_2-k_3-\cdots-k_m)}3^{(b_3+k_3)} \cdots m^{(b_m+k_m)}\end{array}\right] $
in the right hand side of the last equation and let
![]() $k=k_3+\cdots+k_m$
. Then
$k=k_3+\cdots+k_m$
. Then
 \begin{align*}c&= \left(\sum_{i=0}^{t}\binom{\lambda_1+i}{i}(\!-1)^{t-i}\binom{b_2-k}{t-k-i}\right) \binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&= (\!-1)^k\left(\sum_{i=0}^{t-k}\binom{\lambda_1+i}{i}(\!-1)^{t-k-i}\binom{b_2-k}{t-k-i}\right) \binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&= (\!-1)^{k}\binom{\lambda_1-b_2+t}{t-k}\binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m},\end{align*}
\begin{align*}c&= \left(\sum_{i=0}^{t}\binom{\lambda_1+i}{i}(\!-1)^{t-i}\binom{b_2-k}{t-k-i}\right) \binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&= (\!-1)^k\left(\sum_{i=0}^{t-k}\binom{\lambda_1+i}{i}(\!-1)^{t-k-i}\binom{b_2-k}{t-k-i}\right) \binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m}\\&= (\!-1)^{k}\binom{\lambda_1-b_2+t}{t-k}\binom{b_3+k_3}{k_3}\cdots\binom{b_m+k_m}{k_m},\end{align*}
where in the third equality we used the first identity of Lemma 4.1 (2). Thus
where
![]() $k=k_3+\cdots+k_m$
and the sum ranges over all nonnegative integers
$k=k_3+\cdots+k_m$
and the sum ranges over all nonnegative integers
![]() $k_3,...,k_m$
such that
$k_3,...,k_m$
such that
![]() $k \le b_2$
and
$k \le b_2$
and
![]() $k_s \le a_s$
for all
$k_s \le a_s$
for all
![]() $s=3,...,m$
.
$s=3,...,m$
.
By summing with respect to
![]() $T \in \textrm{ST}_{\lambda}({\mu})$
and using Lemma 2.3, we obtain
$T \in \textrm{ST}_{\lambda}({\mu})$
and using Lemma 2.3, we obtain
where the new sum is over all nonnegative integers
![]() $b_2,...,b_m$
such that
$b_2,...,b_m$
such that
![]() $b_i \le \lambda_i (i=2,...,m)$
and
$b_i \le \lambda_i (i=2,...,m)$
and
![]() $b_2+\cdots+b_m=\mu_2$
.
$b_2+\cdots+b_m=\mu_2$
.
Fix
in the right hand side of (1) and let
![]() $q=\mu_2-(b_3+k_3)-\cdots-(b_m+k_m).$
Then
$q=\mu_2-(b_3+k_3)-\cdots-(b_m+k_m).$
Then
![]() $q= b_2-k$
. The coefficient of [S] in (1) is equal to
$q= b_2-k$
. The coefficient of [S] in (1) is equal to
 \begin{align*} &\sum_{k}(\!-1)^k\binom{\lambda_1-q-k+t}{t-k} \sum_{k_3+\cdots+k_m=k}\binom{b_3+k_3}{k_3} \cdots \binom{b_m+k_m}{k_m}\\ &=\sum_{k}(\!-1)^k\binom{\lambda_1-q-k+t}{t-k} \binom{\mu_2 -q}{k}\\& =\binom{\lambda_1-\mu_2+t}{t}\\& =0,\end{align*}
\begin{align*} &\sum_{k}(\!-1)^k\binom{\lambda_1-q-k+t}{t-k} \sum_{k_3+\cdots+k_m=k}\binom{b_3+k_3}{k_3} \cdots \binom{b_m+k_m}{k_m}\\ &=\sum_{k}(\!-1)^k\binom{\lambda_1-q-k+t}{t-k} \binom{\mu_2 -q}{k}\\& =\binom{\lambda_1-\mu_2+t}{t}\\& =0,\end{align*}
where in the first equality we used Lemma 4.1 (1)(a) and in the second equality we used the second identity of Lemma 4.1 (2).
Relations from rows
i
and
![]() $i+1$
(
$i+1$
(
![]() $i>1$
).
$i>1$
).
This computation is similar to the previous one but simpler as there is no straightening. Let
![]() $y=1^{(\lambda_1)}\otimes\cdots\otimes {i}^{(\lambda_i)} \otimes i^{(t)}(i+1)^{(\lambda_{i+1}-t)} \otimes\cdots\otimes m^{(\lambda_m)} \in Im(\square_\lambda),$
where
$y=1^{(\lambda_1)}\otimes\cdots\otimes {i}^{(\lambda_i)} \otimes i^{(t)}(i+1)^{(\lambda_{i+1}-t)} \otimes\cdots\otimes m^{(\lambda_m)} \in Im(\square_\lambda),$
where
![]() $ i>1$
and
$ i>1$
and
![]() $t \le \lambda_{i+1}$
. As before let
$t \le \lambda_{i+1}$
. As before let
The definition of
![]() $\phi_T$
yields
$\phi_T$
yields
By summing with respect to
![]() $T \in \textrm{ST}_{\lambda}(\mu)$
and using Lemma 2.3, we have
$T \in \textrm{ST}_{\lambda}(\mu)$
and using Lemma 2.3, we have
where the new sum ranges over all nonnegative integers
![]() $b_2,...,b_m$
such that
$b_2,...,b_m$
such that
![]() $b_i \le \lambda_i \; (i=2,...,m)$
and
$b_i \le \lambda_i \; (i=2,...,m)$
and
![]() $b_2+\cdots+b_m=\mu_2$
.
$b_2+\cdots+b_m=\mu_2$
.
Fix
in the right hand side of (2) and let
![]() $q=b_i-j$
. The coefficient of [S] in (2) is equal to
$q=b_i-j$
. The coefficient of [S] in (2) is equal to
where in the first equality we used Lemma 4.1 (1)(a).
We have shown thus far that the map
![]() $\psi = \sum_{T \in \textrm{ST}(\lambda, \mu)}\phi_T$
induces a homomorphism of S-modules
$\psi = \sum_{T \in \textrm{ST}(\lambda, \mu)}\phi_T$
induces a homomorphism of S-modules
![]() $\bar{\psi}\,{:}\, \Delta(\lambda) \to \Delta(\mu)$
and it remains to be shown that
$\bar{\psi}\,{:}\, \Delta(\lambda) \to \Delta(\mu)$
and it remains to be shown that
![]() $\bar{\psi} \neq 0$
. Let
$\bar{\psi} \neq 0$
. Let
![]() $z=1^{(\lambda_1)}\otimes\cdots\otimes m^{(\lambda_m)} \in D(\lambda)$
and
$z=1^{(\lambda_1)}\otimes\cdots\otimes m^{(\lambda_m)} \in D(\lambda)$
and
![]() $T \in \textrm{ST}_{\lambda}(\mu).$
Then from the definition of
$T \in \textrm{ST}_{\lambda}(\mu).$
Then from the definition of
![]() $\phi_T$
we have
$\phi_T$
we have
![]() $ \phi_T(x)=[T]$
and hence
$ \phi_T(x)=[T]$
and hence
The right hand side is a sum of distinct basis elements in
![]() $\Delta(\mu)$
(each with coefficient 1) according to Theorem 2.2 and hence nonzero. The proof is complete.
$\Delta(\mu)$
(each with coefficient 1) according to Theorem 2.2 and hence nonzero. The proof is complete.
Remark 5.1 Lyle has shown in [Reference Lyle15], Propositions 2.19 through 2.27 and subsection 3.3, that the homomorphism spaces between Specht modules corresponding to partitions
![]() $\lambda=(\lambda_1,...,\lambda_n), \mu=(\mu_1,\mu_2)$
of r with
$\lambda=(\lambda_1,...,\lambda_n), \mu=(\mu_1,\mu_2)$
of r with
![]() $\mu_2 \le \lambda_1$
, over the complex Hecke algebra
$\mu_2 \le \lambda_1$
, over the complex Hecke algebra
![]() $\mathcal{H}=\mathcal{H}_{\mathbb{C},q}(\mathfrak{S}_r)$
of the symmetric group
$\mathcal{H}=\mathcal{H}_{\mathbb{C},q}(\mathfrak{S}_r)$
of the symmetric group
![]() $\mathfrak{S}_r$
, where q is a complex root of unity, are at most 1 dimensional. Furthermore, she proves exactly when they are nonzero and provides a generator which turns out to correspond to the sum of all standard tableaux in
$\mathfrak{S}_r$
, where q is a complex root of unity, are at most 1 dimensional. Furthermore, she proves exactly when they are nonzero and provides a generator which turns out to correspond to the sum of all standard tableaux in
![]() $\textrm{ST}_{\lambda}(\mu)$
. (Note that our
$\textrm{ST}_{\lambda}(\mu)$
. (Note that our
![]() $\lambda, \mu$
are reversed). In the statement of Theorem 3.1, a similar map is considered and there are some technical similarities between the proof of our main result and [Reference Lyle15]. However, we show in the next section, our modular homomorphism spaces may have dimension greater than 1.
$\lambda, \mu$
are reversed). In the statement of Theorem 3.1, a similar map is considered and there are some technical similarities between the proof of our main result and [Reference Lyle15]. However, we show in the next section, our modular homomorphism spaces may have dimension greater than 1.
6. Homomorphism spaces of dimension greater than 1
As mentioned in Introduction, the first examples of Weyl modules
![]() $\Delta(\lambda),\Delta(\mu)$
such that
$\Delta(\lambda),\Delta(\mu)$
such that
![]() $\dim\textrm{Hom}_S(\Delta(\lambda),\Delta(\mu))>1$
were obtained by Dodge [Reference Dodge6]. More examples were found by Lyle [Reference Lyle14], in fact in the q-Schur algebra setting. The purpose of this section is to observe that the homomorphism spaces of Theorem 3.1 may have dimension
$\dim\textrm{Hom}_S(\Delta(\lambda),\Delta(\mu))>1$
were obtained by Dodge [Reference Dodge6]. More examples were found by Lyle [Reference Lyle14], in fact in the q-Schur algebra setting. The purpose of this section is to observe that the homomorphism spaces of Theorem 3.1 may have dimension
![]() $>1$
, see Corollary 6.2 and Example 6.4 below.
$>1$
, see Corollary 6.2 and Example 6.4 below.
We recall the following special case of the classical nonvanishing result of Carter and Payne [Reference Carter and Payne4]. Here, boxes are raised between consecutive rows. See [Reference Maliakas16], 1.2 Lemma, for a proof of this particular case in our context.
Proposition 6.1. ([Reference Carter and Payne4]). Let
![]() $n \ge r$
. Let
$n \ge r$
. Let
![]() $\lambda, \mu \in \wedge^+(n,r)$
such that for some some
$\lambda, \mu \in \wedge^+(n,r)$
such that for some some
![]() $d>0$
we have
$d>0$
we have
![]() $\mu=(\lambda_1+d,\lambda_2-d,\lambda_3,...,\lambda_m)$
, where
$\mu=(\lambda_1+d,\lambda_2-d,\lambda_3,...,\lambda_m)$
, where
![]() $\lambda=(\lambda_1,...,\lambda_m)$
. Suppose p divides
$\lambda=(\lambda_1,...,\lambda_m)$
. Suppose p divides
![]() $R(\lambda_1-\lambda_2+d+1,d)$
. Then the map
$R(\lambda_1-\lambda_2+d+1,d)$
. Then the map
 \begin{align*} \alpha \,{:}\, D(\lambda_1,\lambda_2,...,\lambda_m) &\xrightarrow{1 \otimes \Delta \otimes 1 } D(\lambda_1,d, \lambda_2-d,...,\lambda_m)\\& \xrightarrow{\eta \otimes 1} D(\lambda_1+d,\lambda_2-d,...,\lambda_m), \end{align*}
\begin{align*} \alpha \,{:}\, D(\lambda_1,\lambda_2,...,\lambda_m) &\xrightarrow{1 \otimes \Delta \otimes 1 } D(\lambda_1,d, \lambda_2-d,...,\lambda_m)\\& \xrightarrow{\eta \otimes 1} D(\lambda_1+d,\lambda_2-d,...,\lambda_m), \end{align*}
where
![]() $\Delta \,{:}\, D(\lambda_2) \to D(d,\lambda_2-d)$
is the indicated diagonalization and
$\Delta \,{:}\, D(\lambda_2) \to D(d,\lambda_2-d)$
is the indicated diagonalization and
![]() $\eta \,{:}\, D(\lambda_1, d) \to D(\lambda_1+d)$
and the indicated multiplication, induces a nonzero homomorphism
$\eta \,{:}\, D(\lambda_1, d) \to D(\lambda_1+d)$
and the indicated multiplication, induces a nonzero homomorphism
![]() $\Delta(\lambda) \to \Delta(\mu)$
. The main result of this section is the following.
$\Delta(\lambda) \to \Delta(\mu)$
. The main result of this section is the following.
Corollary 6.2. Let
![]() $n \ge r$
. Let
$n \ge r$
. Let
![]() $\lambda,\mu \in \wedge^{+}(n,r)$
such that
$\lambda,\mu \in \wedge^{+}(n,r)$
such that
![]() $\lambda=(\lambda_1,...,\lambda_m), \lambda_m \neq 0, m \ge 3$
and
$\lambda=(\lambda_1,...,\lambda_m), \lambda_m \neq 0, m \ge 3$
and
![]() $\mu=(\mu_1, \mu_2)$
. Define
$\mu=(\mu_1, \mu_2)$
. Define
![]() $d=\mu_1-\lambda_1$
and assume
$d=\mu_1-\lambda_1$
and assume
![]() $0<d \le \lambda_2 - \lambda_3$
and
$0<d \le \lambda_2 - \lambda_3$
and
![]() $\mu_2 \le \lambda_1$
. If p divides all of the following integers
$\mu_2 \le \lambda_1$
. If p divides all of the following integers
-
(1)
 $R(\lambda_1 -\mu_2+1,d),$
$R(\lambda_1 -\mu_2+1,d),$
-
(2)
 $R(\lambda_i+1,\lambda_{i+1}), \; i=2,...,m-1,$
$R(\lambda_i+1,\lambda_{i+1}), \; i=2,...,m-1,$
-
(3)
 $R(\lambda_1 -\lambda_2+d+1,d), $
$R(\lambda_1 -\lambda_2+d+1,d), $
-
(4)
 $R(\lambda_2-d+1,\lambda_3),$
$R(\lambda_2-d+1,\lambda_3),$
then the dimension of the K-vector space
![]() $\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu))$
is at least 2.
$\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu))$
is at least 2.
Proof. By the first two divisibility conditions, the map
induces a nonzero homomorphism
![]() $\bar{\psi_1}\,{:}\, \Delta(\lambda) \to \Delta(\mu)$
according to Theorem 3.1.
$\bar{\psi_1}\,{:}\, \Delta(\lambda) \to \Delta(\mu)$
according to Theorem 3.1.
Next consider the following maps
as in Proposition 6.1 and
where
![]() $\eta' \,{:}\, D(\lambda_2-d,...,\lambda_m) \to D(\lambda_2-d+\lambda_3+\cdots +\lambda_m)$
is the indicated multiplication.
$\eta' \,{:}\, D(\lambda_2-d,...,\lambda_m) \to D(\lambda_2-d+\lambda_3+\cdots +\lambda_m)$
is the indicated multiplication.
Under assumption (3), we have that
![]() $\alpha$
induces a nonzero map
$\alpha$
induces a nonzero map
according to Proposition 6.1
Under assumptions (2) and (4), we have that
![]() $\beta$
induces a nonzero map
$\beta$
induces a nonzero map
according to Theorem 2.1
Consider the composition
![]() $\bar{\psi_2} =\bar{\beta}\bar{\alpha} \,{:}\, \Delta(\lambda) \to \Delta(\mu)$
depicted below, where Weyl modules are indicated by the diagrams of the corresponding partitions.
$\bar{\psi_2} =\bar{\beta}\bar{\alpha} \,{:}\, \Delta(\lambda) \to \Delta(\mu)$
depicted below, where Weyl modules are indicated by the diagrams of the corresponding partitions.

It remains to be shown that the homomorphisms
![]() $\bar\psi_1, \bar\psi_2$
are linearly independent. Let
$\bar\psi_1, \bar\psi_2$
are linearly independent. Let
![]() $z=d^{\prime}_{\lambda}(1^{(\lambda_1)}\otimes\cdots\otimes m^{(\lambda_m)}) \in \Delta(\lambda)$
. From the definitions of the maps, we have
$z=d^{\prime}_{\lambda}(1^{(\lambda_1)}\otimes\cdots\otimes m^{(\lambda_m)}) \in \Delta(\lambda)$
. From the definitions of the maps, we have
and
It is clear that
![]() $\begin{array}{l} 1^{(\lambda_1)}2^{(d)} \\ 2^{(\lambda_2-d)} \cdots m^{(\lambda_m)}\end{array} \in \textrm{ST}_{\lambda}(\mu).$
Since
$\begin{array}{l} 1^{(\lambda_1)}2^{(d)} \\ 2^{(\lambda_2-d)} \cdots m^{(\lambda_m)}\end{array} \in \textrm{ST}_{\lambda}(\mu).$
Since
![]() $\lambda_3>0$
, the set
$\lambda_3>0$
, the set
![]() $\textrm{ST}_{\lambda}(\mu)$
contains at least two elements. Hence, from the above equations and Theorem 2.2, it follows that the maps
$\textrm{ST}_{\lambda}(\mu)$
contains at least two elements. Hence, from the above equations and Theorem 2.2, it follows that the maps
![]() $\bar\psi_1, \bar\psi_2$
are linearly independent.
$\bar\psi_1, \bar\psi_2$
are linearly independent.
Remark The assumptions of Corollary 6.2 imply that for the corresponding Specht modules we have
![]() $ \dim \textrm{Hom}_{\mathfrak{S}_r}(\textrm{Sp} (\mu),\textrm{Sp} (\lambda)) \ge 2.$
See Remark 3.2.
$ \dim \textrm{Hom}_{\mathfrak{S}_r}(\textrm{Sp} (\mu),\textrm{Sp} (\lambda)) \ge 2.$
See Remark 3.2.
Example 6.3. Let p be a prime and a an integer such that
![]() $a \ge (p^2+1)(p-1)$
and
$a \ge (p^2+1)(p-1)$
and
Consider the following partitions
where
![]() $p-1$
appears
$p-1$
appears
![]() $p^2$
times as a row in
$p^2$
times as a row in
![]() $\lambda$
. Using Lemma 3.4, it easily follows that the assumptions (1) - (4) of Corollary 6.2 are satisfied. For example, we have
$\lambda$
. Using Lemma 3.4, it easily follows that the assumptions (1) - (4) of Corollary 6.2 are satisfied. For example, we have
and hence by Lemma 3.3,
![]() $d=p$
divides
$d=p$
divides
![]() $R(\lambda_1 - \mu_{2}+1,d)$
which is assumption (1). Thus,
$R(\lambda_1 - \mu_{2}+1,d)$
which is assumption (1). Thus,
![]() $\dim\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \ge 2.$
Footnote
1
$\dim\textrm{Hom}_S(\Delta(\lambda), \Delta(\mu)) \ge 2.$
Footnote
1
For
![]() $p=2$
, the least a that satisfies the above requirements is
$p=2$
, the least a that satisfies the above requirements is
![]() $a=8$
and thus we have the partitions
$a=8$
and thus we have the partitions
![]() $\lambda=(8,3,1,1,1,1), \mu=(10,5)$
. This pair appears in Example 4, Subsection 2.3, of Lyle’s paper [Reference Lyle15] which prompted us to consider Corollary 6.2 and in particular the composition
$\lambda=(8,3,1,1,1,1), \mu=(10,5)$
. This pair appears in Example 4, Subsection 2.3, of Lyle’s paper [Reference Lyle15] which prompted us to consider Corollary 6.2 and in particular the composition
![]() $\bar{\psi_2} =\bar{\beta}\bar{\alpha} \,{:}\, \Delta(\lambda) \to \Delta(\mu)$
.
$\bar{\psi_2} =\bar{\beta}\bar{\alpha} \,{:}\, \Delta(\lambda) \to \Delta(\mu)$
.
Conflict of interest
The authors declare they have no conflict of interest.