Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T06:41:33.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On generalized braid groups

Published online by Cambridge University Press:  18 May 2009

A. K. Napthine  and
Stephen J. Pride
A. K. Napthine
Affiliation:
Minster School, Nottingham Road, Southwell NG25 OMG University of Glasgow, Department of Mathematics, University Gardens, Glasgow, G12 8QW
Stephen J. Pride
Affiliation:
Minster School, Nottingham Road, Southwell NG25 OMG University of Glasgow, Department of Mathematics, University Gardens, Glasgow, G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Braid groups were introduced by Artin [1]. These groups have been studied extensively—see [2], [9] and the references cited there. Recently work has been done on “circular” braid groups and other “braid-like” groups [7], [10]. In this paper we formulate the concept of a generalized braid group, and we begin a study of the structure of such groups. In particular for such a group G1, there is a homomorphism from G onto the infinite cyclic group, the kernel of which is the derived group G1 of G. We study G1. Our results generalize results of Gorin and Lin [5], who considered the case when G is a classical braid group B(n ≥ 3). They showed that 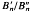is free abelian of rank 2 if n = 3, 4 and is trivial if n ≥ 5. They also showed that 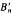is finitely presented.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 2 , July 1986 , pp. 199 - 209
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Artin, E., Theorie der Zöpfe, Abh. Math. Sem. Univ. Hamburg 4 (1925), 47–72.CrossRefGoogle Scholar
2.Birman, J. S., Braids, Links and Mapping Class Groups (Annals of Mathematics Studies 82, Princeton University Press, 1974).Google Scholar
3.Bollobás, B., Graph Theory (Graduate Texts in Mathematics 63, Springer-Verlag, 1979).CrossRefGoogle Scholar
4.Cohen, D., Combinatorial Group Theory: A Topological Approach (Queen Mary College Mathematics Notes).Google Scholar
5.Gorin, E. A. and Lin, V. Ja., Algebraic equations with continuous coefficients and some problems of the algebraic theory of braids, Math. USSR-Sb. 7 (1969), 569–596.CrossRefGoogle Scholar
6.Howie, J. and Pride, S. J., A spelling theorem for staggered generalized 2-complexes, with applications, Invent. Math. 76 (1984), 55–74.CrossRefGoogle Scholar
7.Johnson, D. L., Analogues of the braid group, Proceedings of the Conference Groups-Korea 1983 (Lecture Notes in Mathematics 1098, Springer-Verlag, 1984).Google Scholar
8.Lyndon, R. C. and Schupp, P. E., Combinatorial Group Theory (Springer-Verlag, 1977).Google Scholar
9.Magnus, W., Braid groups: a survey, Proceedings of the Second International Conference on the Theory of Groups (Lecture Notes in Mathematics 372, Springer-Verlag, 1974).CrossRefGoogle Scholar
10.Napthine, A. K., Analogues of the braid group whose graphs are stars, Proc. Edinburgh Math. Soc. (2) 28 (1985), 35–39.CrossRefGoogle Scholar
11.Pride, S. J., Equivalences of combinatorial 2-complexes, in preparation.Google Scholar
12.Serre, J-P., Trees (Springer-Verlag, 1980).CrossRefGoogle Scholar
13.Stillwell, J., Classical Topology and Combinatorial Group Theory (Graduate Texts in Mathematics 72, Springer-Verlag, 1980).CrossRefGoogle Scholar
14.Zieschang, H., Vogt, E. and Coldewey, H.-D., Surfaces and Planar Discontinuous Groups (Lecture Notes in Mathematics 835, Springer-Verlag, 1980).CrossRefGoogle Scholar