Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T19:30:42.551Z Has data issue: false hasContentIssue false
  • English
  • Français

On Differences of Unitarily Equivalent Self-Adjoint Operators†

Published online by Cambridge University Press:  18 May 2009

C. R. Putnam
C. R. Putnam
Affiliation:
Purdue University, Lafayette, Indiana, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. All operators considered in this paper are bounded operators on a Hilbert space. In case A and B are self-adjoint, certain conditions on A, B and their difference

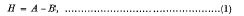
assuring the unitary equivalence of Aand B,

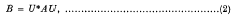
have recently been obtained by Rosenblum [6] and Kato [2]. The present paper will consider the problem of investigating consequences of an assumed relation of type (2) for some unitary U together with an additional hypothesis that the difference H of (1) be non-negative, so that

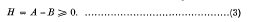
First, it is easy to see that if only (2) and (3) are assumed, thereby allowing H = 0, relation (2) can hold for A arbitrary with U = I (identity) and B = A. If H = 0 in (3) is not allowed, however (an impossible assumption in the finite dimensional case, incidentally, since then the trace of H is zero and hence H = 0), it will be shown, among other things, that any unitary operator U for which (2) and (3) hold must have a spectrum with a positive measure (as a consequence of (i) of Theorem 2 below). Moreover A (hence B) cannot differ from a completely continuous operator by a constant multiple of the identity (Theorem 1). In case 0 is not in the point spectrum of H, then U is even absolutely continuous (see (iv) of Theorem 2). In § 4, applications to semi-normal operators will be given.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 4 , Issue 3 , January 1960 , pp. 103 - 107
Copyright
Copyright © Glasgow Mathematical Journal Trust 1960

References

1.Kato, T., On finite-dimensional perturbations of self-adjoint operators, J. Math. Soc. Japan, 9 (1957), 239–249.CrossRefGoogle Scholar
2.Kato, T., Perturbation of continuous spectra by trace class operators, Proc. Japan Academy, 33 (1957), 260–264.Google Scholar
3.Putnam, C. R., On commutators and Jacobi matrices, Proc. American Math. Soc., 7 (1956), 1026–1030.CrossRefGoogle Scholar
4.Putnam, C. R., On semi-normal operators, Pacific J. Math. 7 (1957), 1649–1652.CrossRefGoogle Scholar
5.Putnam, C. R., Commutators and absolutely continuous operators, Trans. American Math. Soc., 87 (1958), 513–525.CrossRefGoogle Scholar
6.Rosenblum, M., Perturbation of the continuous spectrum and unitary equivalence, Pacific J. Math., 7 (1957), 997–1010.CrossRefGoogle Scholar
7.Woyl, H., Über beschränkte quadratische Formen, deren Differenz vollstetig ist, Rend. Oirc. Math. Palermo, 27 (1909), 373–392.CrossRefGoogle Scholar