Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:18:13.175Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CONJUGACY CLASSES OF THE KLEIN SIMPLE GROUP IN CREMONA GROUP

Part of: Birational geometry

Published online by Cambridge University Press:  10 June 2016

HAMID AHMADINEZHAD
HAMID AHMADINEZHAD*
Affiliation:
School of Mathematics, University of Bristol, Bristol, BS8 1TW, United Kingdom e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider countably many three-dimensional PSL2(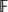$\mathbb{F}$7)-del Pezzo surface fibrations over ℙ1. Conjecturally, they are all irrational except two families, one of which is the product of a del Pezzo surface with ℙ1. We show that the other model is PSL2(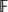$\mathbb{F}$7)-equivariantly birational to ℙ2×ℙ1. Based on a result of Prokhorov, we show that they are non-conjugate as subgroups of the Cremona group Cr3(ℂ).

MSC classification

Primary: 14E07: Birational automorphisms, Cremona group and generalizations
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 2 , May 2017 , pp. 395 - 400
Copyright
Copyright © Glasgow Mathematical Journal Trust 2016 

References

REFERENCES

1. Ahmadinezhad, H., Singular del Pezzo fibrations and birational rigidity, in Automorphisms in birational and affine geometry, Springer Proceedings in Mathematics & Statistics, vol. 79 (Ivan, C., Ciro, C., Hubert, F., James, M., Yuri, G. P., Mikhail, Z., Editors) (Springer International Publishing, Switzerland, 2014), 3–15.Google Scholar
2. Beauville, A., p-elementary subgroups of the Cremona group, J. Algebra 314 (2) (2007), 553–564.CrossRefGoogle Scholar
3. Belousov, G., Log del Pezzo surfaces with simple automorphism groups, Proc. Edinb. Math. Soc. (2) 58 (1) (2015), 33–52.Google Scholar
4. Bogomolov, F. and Prokhorov, Y., On stable conjugacy of finite subgroups of the plane Cremona group, I, Cent. Eur. J. Math. 11 (12) (2013), 2099–2105.Google Scholar
5. Cheltsov, I., Two local inequalities, Izv. Ross. Akad. Nauk Ser. Mat. 78 (2) (2014), 167–224.Google Scholar
6. Cheltsov, I. and Shramov, C., Three embeddings of the Klein simple group into the Cremona group of rank three, Transform. Groups 17 (2) (2012), 303–350.CrossRefGoogle Scholar
7. Cheltsov, I. and Shramov, C., Five embeddings of one simple group, Trans. Amer. Math. Soc. 366 (3) (2014), 1289–1331.CrossRefGoogle Scholar
8. Grinenko, M., On the birational rigidity of some pencils of del Pezzo surfaces, J. Math. Sci. (New York) 102 (2) (2000), 3933–3937, Algebraic geometry, 10. MR 1794170 (2001j:14012)CrossRefGoogle Scholar
9. Prokhorov, Y., Simple finite subgroups of the Cremona group of rank 3, J. Algebr. Geom. 21 (3) (2012), 563–600.Google Scholar
10. Prokhorov, Y., On stable conjugacy of finite subgroups of the plane Cremona group, II, Michigan Math. J., 64 (2) (2015), 293–318.Google Scholar
11. Pukhlikov, A., Birationally rigid varieties, Mathematical surveys and monographs, vol. 190 (American Mathematical Society, Providence, RI, 2013).Google Scholar
12. Serre, J.-P., A Minkowski-style bound for the orders of the finite subgroups of the Cremona group of rank 2 over an arbitrary field, Mosc. Math. J. 9 (1) (2009), 193–208, back matter.Google Scholar