Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-04T13:30:00.579Z Has data issue: false hasContentIssue false
  • English
  • Français

On commutativity of C*-algebras

Published online by Cambridge University Press:  18 May 2009

C.-S. Lin
C.-S. Lin
Affiliation:
Department of Mathematics, Bishop's University, Lennoxville, Quebec, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Two numerical characterizations of commutativity for C*-algebra 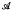(acting on the Hilbert space H) were given in [1]; one used the norms of self-adjoint operators in 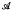(Theorem 2), and the other the numerical index of 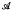(Theorem 3). In both cases the proofs were based on the result of Kaplansky which states that if the only nilpotent operator in 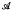is 0, then 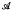is commutative ([2] 2.12.21, p. 68). Of course the converse also holds.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 29 , Issue 1 , January 1987 , pp. 93 - 97
Copyright
Copyright © Glasgow Mathematical Journal Trust 1987

References

REFERENCES

1.Crabb, M. J., Duncan, J. and McGregor, C. M., Characterizations of commutativity for C*-algebras, Glasgow Math. J. 15 (1974), 172–175.CrossRefGoogle Scholar
2.Dixmier, J., C*-algebras, (North-Holland, 1977).Google Scholar
3.Holbrook, J. A. R., On the power-bounded operators of Sz-Nagy and Foias, Acta Sci. Math., 29 (1968), 299–310.Google Scholar
4.Sz-Nagy, B. and Foias, C., Harmonic analysis of operators on Hilbert Space, (Akadémiai Kiadó, Budapest, 1970).Google Scholar