Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-06T02:12:15.938Z Has data issue: false hasContentIssue false
  • English
  • Français

On bornological products

Published online by Cambridge University Press:  18 May 2009

A. P. Robertson
A. P. Robertson
Affiliation:
The University, Keele
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that, provided that the indexing set I is not too large, the product

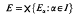
of a family of bornological locally convex topological vector spaces Eαis bornological. Products of bornological spaces were first studied by Mackey [3]. He reduced the problem to the study of R1, showing that this space is bornological if and only if I satisfies a certain condition, related to a problem in measure theory posed by Ulam [5]. We shall therefore call it the Mackey-Ulam condition on I. A similar study of the spaces R1 is to be found in the paper [4] by Simons; see also [1, Ch. IV, §6, exercise 3].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 11 , Issue 1 , January 1970 , pp. 37 - 40
Copyright
Copyright © Glasgow Mathematical Journal Trust 1970

References

REFERENCES

1.Grothendieck, A., Espaces vectoriels topologiques (Sãao Paulo, 1958).Google Scholar
2.Iyahen, S. O., Semiconvex spaces II, Glasgow Math. J. 10 (1969), 103–105.CrossRefGoogle Scholar
3.Mackey, G. W., Equivalence of a problem in measure theory to a problem in the theory of vector lattices, Bull. Amer. Math. Soc. 50 (1944), 719–722.CrossRefGoogle Scholar
4.Simons, S., The bornological space associated with R1, J. London Math. Soc. 36 (1961), 461–473.CrossRefGoogle Scholar
5.Ulam, S., Zur Masstheorie in der allgemeinen Mengenlehre, Fund. Math. 16 (1930), 140–150.CrossRefGoogle Scholar