Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
BRODERICK, RYAN
FISHMAN, LIOR
and
KLEINBOCK, DMITRY
2011.
Schmidt’s game, fractals, and orbits of toral endomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 31,
Issue. 4,
p.
1095.
Kleinbock, Dmitry
and
Ly, Tue
2016.
Badly approximable S-numbers and absolute Schmidt games.
Journal of Number Theory,
Vol. 164,
Issue. ,
p.
13.
EINSIEDLER, MANFRED
GHOSH, ANISH
and
LYTLE, BEVERLY
2016.
Badly approximable vectors, curves and number fields.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 6,
p.
1851.
Lukyanenko, Anton
and
Vandehey, Joseph
2020.
Intrinsic diophantine approximation in Carnot groups and in the Siegel model of the Heisenberg group.
Monatshefte für Mathematik,
Vol. 192,
Issue. 3,
p.
651.
Sawant, Gaurav
2023.
Weighted badly approximable complex vectors and bounded orbits of certain diagonalizable flows.
International Journal of Number Theory,
Vol. 19,
Issue. 08,
p.
1977.
Sawant, Gaurav
2025.
Hyperplane absolute winning property of bounded orbits under diagonalizable flows on $${\textbf{SL}}_{\textbf {3}}({\pmb {\mathbb {C}}})\varvec{/}{\textbf{SL}}_{\textbf {3}}({\varvec{\mathcal {O}_{\pmb {\mathbb {K}}}}})$$.
Proceedings - Mathematical Sciences,
Vol. 135,
Issue. 1,


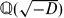 , where
, where 