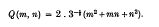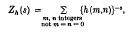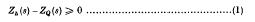Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ennola, Veikko
1964.
On a problem about the Epstein zeta-function.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 60,
Issue. 4,
p.
855.
Ennola, Veikko
1964.
A lemma about the Epstein zeta-function.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 4,
p.
198.
Diananda, P. H.
1964.
Notes on two lemmas concerning the Epstein zeta-function.
Proceedings of the Glasgow Mathematical Association,
Vol. 6,
Issue. 4,
p.
202.
Emersleben, Otto
1967.
Mehrdimensionale Verallgemeinerungen der Eulerschen Konstanten.
Mathematische Nachrichten,
Vol. 34,
Issue. 1-2,
p.
19.
Ryshkov, S. S.
1974.
On the question of final ?-optimality of lattices providing the closest lattice packing of n-dimensional spheres.
Siberian Mathematical Journal,
Vol. 14,
Issue. 5,
p.
743.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Montgomery, Hugh L.
1988.
Minimal theta functions.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 1,
p.
75.
Shushbaev, S. Sh.
1989.
Local minima of the Epstein zeta-function.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 45,
Issue. 1,
p.
83.
Stein, Michael L.
1995.
Locally lattice sampling designs for isotropic random fields.
The Annals of Statistics,
Vol. 23,
Issue. 6,
Orlovskaya, E. V.
1997.
A minimum for the theta function in three variables and the solution of the Rankin-Sobolev problem in a three-dimensional space.
Journal of Mathematical Sciences,
Vol. 83,
Issue. 5,
p.
657.
Chiu, Patrick
1997.
Height of flat tori.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 3,
p.
723.
Sarnak, Peter
and
Strömbergsson, Andreas
2006.
Minima of Epstein’s Zeta function and heights of flat tori.
Inventiones mathematicae,
Vol. 165,
Issue. 1,
p.
115.
COULANGEON, RENAUD
2008.
ON EPSTEIN'S ZETA FUNCTION OF HUMBERT FORMS.
International Journal of Number Theory,
Vol. 04,
Issue. 03,
p.
387.
Fukshansky, Lenny
2009.
On similarity classes of well-rounded sublattices of Z2.
Journal of Number Theory,
Vol. 129,
Issue. 10,
p.
2530.
Zachary, Chase E
and
Torquato, Salvatore
2009.
Hyperuniformity in point patterns and two-phase random heterogeneous media.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2009,
Issue. 12,
p.
P12015.
Gruber, Peter M.
2012.
Application of an idea of Voronoĭ to lattice zeta functions.
Proceedings of the Steklov Institute of Mathematics,
Vol. 276,
Issue. 1,
p.
103.
Sandier, Etienne
and
Serfaty, Sylvia
2012.
From the Ginzburg-Landau Model to Vortex Lattice Problems.
Communications in Mathematical Physics,
Vol. 313,
Issue. 3,
p.
635.
Osting, Braxton
Marzuola, Jeremy
and
Cherkaev, Elena
2015.
An isoperimetric inequality for an integral operator on flat tori.
Illinois Journal of Mathematics,
Vol. 59,
Issue. 3,
Bétermin, Laurent
2016.
Two-Dimensional Theta Functions and Crystallization among Bravais Lattices.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 5,
p.
3236.
Rougerie, Nicolas
and
Serfaty, Sylvia
2016.
Higher‐Dimensional Coulomb Gases and Renormalized Energy Functionals.
Communications on Pure and Applied Mathematics,
Vol. 69,
Issue. 3,
p.
519.