Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T05:23:25.543Z Has data issue: false hasContentIssue false
  • English
  • Français

On a periodic neutral logistic equation

Published online by Cambridge University Press:  18 May 2009

K. Gopalsamy ,
Xue-Zhong He  and
Lizhi Wen
K. Gopalsamy
Affiliation:
School of Information Science, Flinders University, Bedford Park, S.A. 5042, Australia
Xue-Zhong He
Affiliation:
Department of Mathematics, Ningxia University, Yinchuan, P.R. China
Lizhi Wen
Affiliation:
Department of Mathematics, South China Normal University, P.R. China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The oscillatory and asymptotic behaviour of the positive solutions of the autonomous neutral delay logistic equation

with r, c, T, K ∈ (0, ∞) has been recently investigated in [2]. More recently the dynamics of the periodic delay logistic equation

in which r, K are periodic functions of period τ and m is a positive integer is considered in [6]. The purpose of the following analysis is to obtain sufficient conditions for the existence and linear asymptotic stability of a positive periodic solution of a periodic neutral delay logistic equation

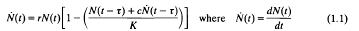
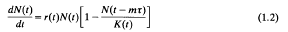
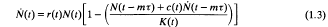
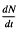in which Ṅ denotes and r, K, c are positive continuous periodic functions of period τ at and m is a positive integer. For the origin and biological relevance of (1.3) we refer to [2].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 3 , September 1991 , pp. 281 - 286
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.El'sgol'ts, L. E. and Norkin, S. B., Introduction to the theory and application of differential equations with deviating arguments (Academic Press, 1973).Google Scholar
2.Gopalsamy, K. and Zhang, B. G., On a neutral delay logistic equation, Dynamic Stability Systems 2 (1988), 183–195.CrossRefGoogle Scholar
3.Halanay, A., Differential equations; stability, oscillations and time lags (Academic Press, 1965), 377–383.Google Scholar
4.Kolmanovskii, V. B. and Nosov, V. R., Stability of functional differential equations (Academic Press, 1986).Google Scholar
5.Yoshizawa, T., Stability theory and the existence of periodic solutions and almost periodic solutions, Applied Mathematical Sciences 14 (Springer-Verlag, 1975).CrossRefGoogle Scholar
6.Zhang, B. G. and Gopalsamy, K., Global attractivity and oscillations in a periodic delay logistic equation, J. Math. Anal. Appl. 150 (1990), 274–283.CrossRefGoogle Scholar