No CrossRef data available.
Article contents
ON A PAIRING BETWEEN SYMMETRIC POWER MODULES
Published online by Cambridge University Press: 02 August 2012
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove, using purely combinatorial methods, that there is a pairing
with an M2(ℚ)-equivariance property.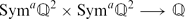 \begin{linenomath}
$$\Sym^a\Q^2\times\Sym^a\Q^2\lra\Q$$
\end{linenomath}
\begin{linenomath}
$$\Sym^a\Q^2\times\Sym^a\Q^2\lra\Q$$
\end{linenomath}
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2012
References
REFERENCES
1.Crane, M., Raising the levels of Hilbert modular forms, PhD Thesis (University of Sheffield, Sheffield, UK, 2007).Google Scholar
2.Jordan, B. and Livné, R., Integral Hodge theory and congruences between modular forms, Duke Math. J. 80 (1995), 419–484.CrossRefGoogle Scholar
3.Kisin, M., Moduli of finite flat group schemes, and modularity, Ann. Math. 170 (2009), 1085–1180.CrossRefGoogle Scholar
4.Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.Google Scholar


