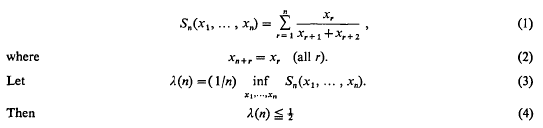Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nowosad, Pedro
1968.
Isoperimetric eigenvalue problems in algebras.
Communications on Pure and Applied Mathematics,
Vol. 21,
Issue. 5,
p.
401.
Malcolm, Michael A.
1971.
A note on a conjecture of L. J. Mordell.
Mathematics of Computation,
Vol. 25,
Issue. 114,
p.
375.
Daykin, David E.
1971.
Inequalities for certain cyclic sums.
Proceedings of the Edinburgh Mathematical Society,
Vol. 17,
Issue. 3,
p.
257.
Godunova, E. K.
and
Levin, V. I.
1973.
Sharpening certain cyclic inequalities.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 14,
Issue. 3,
p.
735.
Diananda, P. H.
1974.
Some cyclic and other inequalities. IV.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 76,
Issue. 1,
p.
183.
Godunova, E. K.
and
Levin, V. I.
1976.
A cyclic sum with 12 terms.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 19,
Issue. 6,
p.
510.
Bushell, P. J.
and
Craven, A. H.
1976.
26.—On Shapiro's Cyclic Inequality.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 75,
Issue. 4,
p.
333.
Troesch, B. A.
1980.
The shooting method applied to a cyclic inequality.
Mathematics of Computation,
Vol. 34,
Issue. 149,
p.
175.
Troesch, B. A.
1985.
On Shapiro’s cyclic inequality for 𝑁=13.
Mathematics of Computation,
Vol. 45,
Issue. 171,
p.
199.
Troesch, B. A.
1989.
The validity of Shapiro’s cyclic inequality.
Mathematics of Computation,
Vol. 53,
Issue. 188,
p.
657.
Clausing, Achim
1992.
General Inequalities 6.
Vol. 103,
Issue. ,
p.
17.
Bushell, Peter J.
1996.
World Congress of Nonlinear Analysts '92.
p.
1523.
Fink, A. M.
1998.
Recent Progress in Inequalities.
p.
241.
Tuan, NguyenMinh
and
Thuong, LeQuy
2009.
On an Extension of Shapiro's Cyclic Inequality.
Journal of Inequalities and Applications,
Vol. 2009,
Issue. 1,
p.
491576.
Choudhury, Projesh Nath
and
Sivakumar, K. C.
2022.
Nesbitt and Shapiro cyclic sum inequalities for positive definite matrices.
Advances in Operator Theory,
Vol. 7,
Issue. 1,