No CrossRef data available.
Article contents
Null, recursively starlike-equivalent decompositions shrink
Published online by Cambridge University Press: 28 October 2022
Abstract
A subset E of a metric space X is said to be starlike-equivalent if it has a neighbourhood which is mapped homeomorphically into 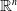 $\mathbb{R}^n$ for some n, sending E to a starlike set. A subset
$\mathbb{R}^n$ for some n, sending E to a starlike set. A subset 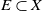 $E\subset X$ is said to be recursively starlike-equivalent if it can be expressed as a finite nested union of closed subsets
$E\subset X$ is said to be recursively starlike-equivalent if it can be expressed as a finite nested union of closed subsets 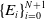 $\{E_i\}_{i=0}^{N+1}$ such that
$\{E_i\}_{i=0}^{N+1}$ such that 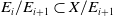 $E_{i}/E_{i+1}\subset X/E_{i+1}$ is starlike-equivalent for each i and
$E_{i}/E_{i+1}\subset X/E_{i+1}$ is starlike-equivalent for each i and 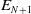 $E_{N+1}$ is a point. A decomposition
$E_{N+1}$ is a point. A decomposition 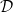 $\mathcal{D}$ of a metric space X is said to be recursively starlike-equivalent, if there exists
$\mathcal{D}$ of a metric space X is said to be recursively starlike-equivalent, if there exists 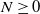 $N\geq 0$ such that each element of
$N\geq 0$ such that each element of 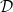 $\mathcal{D}$ is recursively starlike-equivalent of filtration length N. We prove that any null, recursively starlike-equivalent decomposition
$\mathcal{D}$ is recursively starlike-equivalent of filtration length N. We prove that any null, recursively starlike-equivalent decomposition 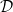 $\mathcal{D}$ of a compact metric space X shrinks, that is, the quotient map
$\mathcal{D}$ of a compact metric space X shrinks, that is, the quotient map 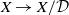 $X\to X/\mathcal{D}$ is the limit of a sequence of homeomorphisms. This is a strong generalisation of results of Denman–Starbird and Freedman and is applicable to the proof of Freedman’s celebrated disc embedding theorem. The latter leads to a multitude of foundational results for topological 4-manifolds, including the four-dimensional Poincaré conjecture.
$X\to X/\mathcal{D}$ is the limit of a sequence of homeomorphisms. This is a strong generalisation of results of Denman–Starbird and Freedman and is applicable to the proof of Freedman’s celebrated disc embedding theorem. The latter leads to a multitude of foundational results for topological 4-manifolds, including the four-dimensional Poincaré conjecture.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust



