Let Ω: be a compact Hausdorff space, let E be a Banach space, and let C(Ω, E) stand for the Banach space of continuous E-valued functions on Ω under supnorm. It is well known [3, p. 182] that if F is a Banach space then any bounded linear operator T:C(Ω, E)→ F has a finitely additive vector measure G defined on the σ-field of Borel subsets of Ω with values in the space ℒ(E, F**) of bounded linear operators from E to the second dual F** of F. The measure G is said to represent T. The purpose of this note is to study the interplay between certain properties of the operator T and properties of the representing measure G. Precisely, one of our goals is to study when one can characterize nuclear operators in terms of their representing measures. This is of course motivated by a well-known theorem of L. Schwartz [5] (see also [3, p. 173]) concerning nuclear operators on spaces C(Ω) of continuous scalar-valued functions. The study of nuclear operators on spaces C(Ω, E) of continuous vector-valued functions was initiated in [1], where the author extended Schwartz's result in case E* has the Radon-Nikodym property. In this paper, we will show that the condition on E* to have the Radon-Nikodym property is necessary to have a Schwartz's type theorem. This leads to a new characterization of dual spaces E* with the Radon-Nikodym property. In [2], it was shown that if T:C(Ω, E)→ F is nuclear than its representing measure G takes its values in the space 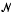(E, F) of nuclear operators from E to F. One of the results of this paper is that if T:C(Ω, E)→ F is nuclear then its representing measure G is countably additive and of bounded variation as a vector measure taking its values in 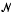(E, F) equipped with the nuclear norm. Finally, we show by easy examples that the above mentioned conditions on the representing measure G do not characterize nuclear operators on C(Ω, E) spaces, and we also look at cases where nuclear operators are indeed characterized by the above two conditions. For all undefined notions and terminologies, we refer the reader to [3].