Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Louboutin, Stéphane
2009.
On the divisibility of the class number of imaginary quadratic number fields.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 12,
p.
4025.
KISHI, YASUHIRO
2010.
NOTE ON THE DIVISIBILITY OF THE CLASS NUMBER OF CERTAIN IMAGINARY QUADRATIC FIELDS – CORRIGENDUM.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 1,
p.
207.
KISHI, YASUHIRO
2010.
ON THE IDEAL CLASS GROUP OF CERTAIN QUADRATIC FIELDS.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 3,
p.
575.
ITO, AKIKO
2011.
REMARKS ON THE DIVISIBILITY OF THE CLASS NUMBERS OF IMAGINARY QUADRATIC FIELDS .
Glasgow Mathematical Journal,
Vol. 53,
Issue. 2,
p.
379.
Ito, Akiko
2011.
A note on the divisibility of class numbers of imaginary quadratic fields $\mathbf{Q}(\sqrt{a^{2} - k^{n}})$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 87,
Issue. 9,
MINHUI, ZHU
and
TINGTING, WANG
2012.
THE DIVISIBILITY OF THE CLASS NUMBER OF THE IMAGINARY QUADRATIC FIELD .
Glasgow Mathematical Journal,
Vol. 54,
Issue. 1,
p.
149.
Ito, Akiko
2015.
Notes on the divisibility of the class numbers of imaginary quadratic fields $$\mathbb {Q}(\sqrt{3^{2e} - 4k^n})$$ Q ( 3 2 e - 4 k n ).
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 85,
Issue. 1,
p.
1.
Chakraborty, Kalyan
Hoque, Azizul
and
Sharma, Richa
2018.
Advances in Mathematical Inequalities and Applications.
p.
247.
Chakraborty, K.
Hoque, A.
Kishi, Y.
and
Pandey, P.P.
2018.
Divisibility of the class numbers of imaginary quadratic fields.
Journal of Number Theory,
Vol. 185,
Issue. ,
p.
339.
Kalita, Himashree
and
Saikia, Helen K.
2020.
Class Groups of Number Fields and Related Topics.
p.
141.
Hoque, Azizul
2021.
On the Exponents of Class Groups of Some Families of Imaginary Quadratic Fields.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 4,
Pandey, Prem Prakash
2021.
NON‐DIVISIBILITY OF CLASS NUMBERS AND PRIME VALUES OF POLYNOMIALS.
Mathematika,
Vol. 67,
Issue. 3,
p.
569.
Kim, Kwang-Seob
2022.
Some Remarks on the Divisibility of the Class Numbers of Imaginary Quadratic Fields.
Mathematics,
Vol. 10,
Issue. 14,
p.
2488.
KRISHNAMOORTHY, SRIlAKSHMI
and
PASUPULATI, SUNIL KUMAR
2022.
NOTE ON THE p-DIVISIBILITY OF CLASS NUMBERS OF AN INFINITE FAMILY OF IMAGINARY QUADRATIC FIELDS.
Glasgow Mathematical Journal,
Vol. 64,
Issue. 2,
p.
352.
Mawlood Taher, Huda
Mohamed, Ali Hasan
and
Saeed Yaseen, Selda
2023.
Prevalence of Intestinal Parasitic Infections among children in Kirkuk City, Iraq..
Bionatura,
Vol. 8,
Issue. CSS 1,
p.
1.
Lee, Siyun
Lee, Yoonjin
and
Yoo, Jinjoo
2023.
Infinite families of class groups of quadratic fields with 3-rank at least one: quantitative bounds.
International Journal of Number Theory,
Vol. 19,
Issue. 03,
p.
621.
Kim, Kwang-Seob
and
König, Joachim
2024.
On -unramified extensions over imaginary quadratic fields.
Glasgow Mathematical Journal,
Vol. 66,
Issue. 1,
p.
119.
Banerjee, Kalyan
and
Hoque, Azizul
2024.
Chow groups, pull back and class groups.
Monatshefte für Mathematik,
Vol. 205,
Issue. 3,
p.
433.
Jin, Seokho
and
Kim, Kwang-Seob
2025.
A new family of imaginary quadratic fields with class number divisible by 5.
The Ramanujan Journal,
Vol. 66,
Issue. 3,
Agnihotri, Rishabh
Laishram, Shanta
and
Mishra, Mohit
2025.
On the class number of $${\mathbb {Q}}(\sqrt{(2^ra)^{2}- y^p})$$.
The Ramanujan Journal,
Vol. 66,
Issue. 1,


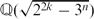 is divisible by
is divisible by 