Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T01:05:53.193Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the characterisation of eigencurves for certain two parameter eigenvalue problems in ordinary differential equations

Published online by Cambridge University Press:  18 May 2009

Patrick J. Browne  and
B. D. Sleeman
Patrick J. Browne
Affiliation:
Department of Mathematics and Statistics University of Calgary Calgary Albert a Canada T2N 1N4
B. D. Sleeman
Affiliation:
Department of Mathematics and Computer Science University of Dundee Dundee Dd1 4Hn Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are interested in two parameter eigenvalue problems of the form

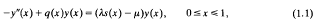
subject to Dirichlet boundary conditions

The weight function 5 and the potential q will both be assumed to lie in L2[0,1]. The problem (1.1), (1.2) generates eigencurves

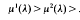
in the sense that for any fixed λ, ν(λ) is the nth eigenvalue ν, (according to oscillation indexing) of (1.1), (1.2). These curves are in fact analytic functions of λ and have been the object of considerable study in recent years. The survey paper [1] provides background in this area and itemises properties of eigencurves.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 1 , January 1993 , pp. 63 - 67
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Browne, P. J., Two parameter eigencurve theory, in Ordinary and Partial Differential Equations Vol. II, Pitman Research Notes in Mathematics No. 216, (Longman, 1989), 52–60.Google Scholar
2.Poschel, J. and Trubowitz, E., Inverse spectral theory, (Academic Press, 1987).Google Scholar