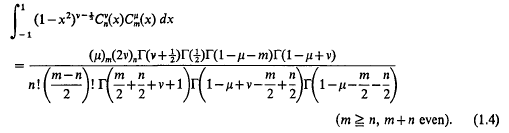Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-02-05T06:55:40.309Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the associated Legendre polynomials

Published online by Cambridge University Press:  18 May 2009

P. R. Khandekar
P. R. Khandekar
Affiliation:
Motilal Vlgyan MahavidyalayaBhopal (M.P.)India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is paper gives what appears to be a new Rodrigues’ formula for the Associated Legendre Polynomials defined by [5, p. 122]

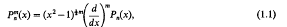
with the restriction that m is an even positive integer, which helps to evaluate some integrals. Putting m = 2k in (1.1) and replacing Pn(x) by the Gegenbauer Polynomial 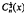and using [3, p. 176]

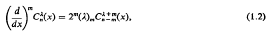
We obtain

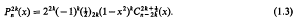
Putting a =v–½ in the relation [4, p. 283]

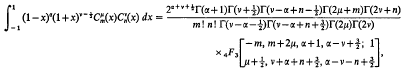
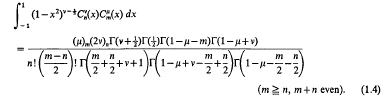
We get

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 3 , January 1964 , pp. 156 - 160
Copyright
Copyright © Glasgow Mathematical Journal Trust 1964

References

REFERENCES

1.Bailey, W. N., Generalised hypergeometric series (Cambridge, 1935).Google Scholar
2.Derkafĉ, P. H., An application of the Legendre polynomial, Ukrain. Mat. Ž. 12 (1960), 466–471; M.R. 25, 3203.Google Scholar
3.Erdélyi, A. et al. , Higher transcendental functions, Vol. II (New York, 1953).Google Scholar
4.Erdélyi, A. et al. , Tables of integral transforms, Vol. II (New York, 1954).Google Scholar
5.MacRobert, T. M., Spherical harmonics (London, 1947).Google Scholar