Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T01:09:05.618Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Regular Coverings of Closed Orientable Surfaces

Published online by Cambridge University Press:  18 May 2009

Jens Mennicke
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The object of this note is to study the regular coverings of the closed orientable surface of genus 2.

Let the closed orientable surface Fh of genus h be a covering of F2 and let 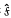and f be the fundamental groups respectively. Then 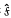is a subgroup of f of index n = h − 1. A covering is called regular if 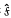is normal in f.

Conversely, let 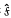be a normal subgroup of f of finite index. Then there is a uniquely determined regular covering Fh such that 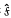is the fundamental group of Fh. The covering Fh is an orientable surface. Since the index n of 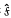in f is supposed to be finite, Fh is closed, and its genus is given by n = h − 1.

The fundamental group f can be defined by

.

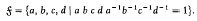Type
Research Article
Information
Glasgow Mathematical Journal , Volume 5 , Issue 2 , July 1961 , pp. 49 - 66
Copyright
Copyright © Glasgow Mathematical Journal Trust 1961

References

1.Bachmann, F., Aufbau der Geometrie aus dem Spiegelungsbegriff (Heidelberg, 1959).CrossRefGoogle Scholar
2.Bergau, P. and Mennicke, J., Über topologische Abbildungen der Brezelfläche vom Geschlecht 2, Math. Zeit. 74 (1960), 414–435.CrossRefGoogle Scholar
3.Brenner, J. L., The linear homogeneous group, Ann. of Math. 39 (1938), 472–493.CrossRefGoogle Scholar
4.Brenner, J. L., The linear homogeneous group, II, Ann. of Math. 45 (1944), 101–109.CrossRefGoogle Scholar
5.Brenner, J. L., The linear homogeneous group, III, Ann. of Math. 71 (1960), 210–223.CrossRefGoogle Scholar
6.Coxeter, H. S. M. and Moser, J., Generators and relations for discrete groups (Erg. d. Math., N. F. 14, 1957).CrossRefGoogle Scholar
7.Dickson, L. E., Linear groups, with an exposition of the Galois field theory (New York, 1958).Google Scholar
8.Fenchel, W., On the projective geometric foundations of the non-Euclidean geometry, Mat. Tidsskr. B. 1941, 18–30 (Danish).Google Scholar
9.Goeritz, L., Die Abbildungen der Brezelfläche und der Vollbrezel vom Geschlecht 2, Hamb. Abh. 9 (1933), 244–259.CrossRefGoogle Scholar
10.Jones, B. W., The arithmetic theory of quadratic forms (New York, 1950).CrossRefGoogle Scholar
11.Klein, F., Elementary mathematics from an advanced standpoint—Geometry (New York, 1939).Google Scholar
12.Reiner, I., Normal subgroups of the unimodular group, Illinois J. Math. 2 (1958), 142–144.CrossRefGoogle Scholar
13.Seifert, H. and Threlfall, W., Lehrbuch der Topologie (New York, 1947).Google Scholar
14.Waerden, B. L. Van der, Gruppen von linearen Transformationen (Erg. d. Math. 4, 1935).CrossRefGoogle Scholar
15.Zassenhaus, H., The theory of groups (New York, 2nd ed. 1958).Google Scholar