Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T20:21:20.466Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on reductions of ideals relative to an Artinian module

Published online by Cambridge University Press:  18 May 2009

A.-J. Taherizadeh
A.-J. Taherizadeh
Affiliation:
Department of Mathematics, Teacher Training University, 49 Mofateh Ave, Tehran, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The concept of reduction and integral closure of ideals relative to Artinian modules were introduced in [7]; and we summarize some of the main aspects now.

Let A be a commutative ring (with non-zero identity) and let a, b be ideals of A. Suppose that M is an Artinian module over A. We say that a is a reduction of b relative to M if a ⊆ b and there is a positive integer s such that

)O:Mabs)=(O:Mbs+l).

An element x of A is said to be integrally dependent on a relative to M if there exists n y ℕ(where ℕ denotes the set of positive integers) such that

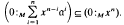
It is shown that this is the case if and only if a is a reduction of a+Ax relative to M; moreover

ᾱ={x ɛ A: xis integrally dependent on a relative to M}

is an ideal of A called the integral closure of a relative to M and is the unique maximal member of

℘ = {b: b is an ideal of A which has a as a reduction relative to M}.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 219 - 224
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Kirby, D., Artinian modules and Hilbert polynomials, Quart. J. Math. Oxford Ser. (2) 24 (1973), 47–57.CrossRefGoogle Scholar
2.Macdonald, I. G., Secondary representation of modules over a commutative ring, Sympos. Math. 11 (1973), 23–43.Google Scholar
3.Mirbagheri, A. and Ratliff, L. J. Jr, On the relevant transform and the relevant component of an ideal, J. Algebra 111 (1987), 507–519.CrossRefGoogle Scholar
4.Ooishi, A., Matlis duality and the width of a module, Hiroshima Math. J. 6 (1976), 573–587.CrossRefGoogle Scholar
5.Ratliff, L. J. Jr and Rush, David E., Two notes on reduction of ideals, Indiana Univ. Math. J. 27 (1978), 929–934.CrossRefGoogle Scholar
6.Sharp, R. Y., Asymptotic behaviour of certain sets of attached prime ideals, J. London Math. Soc. (2) 34 (1986), 212–218.CrossRefGoogle Scholar
7.Sharp, R. Y. and Taherizadeh, A.-J., Reductions and integral closures of ideals relative to an Artinian module, J. London Math. Soc. (2) 37 (1988), 203–218.CrossRefGoogle Scholar
8.Taherizadeh, A.-J., Behaviour of ideals relative to Artinian modules over commutative rings (Ph.D. thesis, University of Sheffield, 1987).Google Scholar
9.Taherizadeh, A.-J., On Asymptotic values of certain sets of attached prime ideals, Glasgow Math. J. 30 (1988), 293–300.CrossRefGoogle Scholar