Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T00:15:27.876Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON RANK TWO STABLE BUNDLES OVER SURFACES

Part of: Surfaces and higher-dimensional varieties Families, fibrations Curves

Published online by Cambridge University Press:  28 June 2021

GRACIELA REYES-AHUMADA ,
L. ROA-LEGUIZAMÓN  and
H. TORRES-LÓPEZ
GRACIELA REYES-AHUMADA
Affiliation:
CONACYT – U. A. Matemáticas, U. Autónoma de Zacatecas, Calzada Solidaridad entronque Paseo a la Bufa, C.P. 98000, Zacatecas, Zac. Mexico e-mail: [email protected]
L. ROA-LEGUIZAMÓN
Affiliation:
Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Edificio C3, Ciudad Universitaria, C.P. 58040 Morelia, Mich. Mexico e-mail: [email protected]
H. TORRES-LÓPEZ
Affiliation:
CONACYT - U. A. Matemáticas, U. Autónoma de Zacatecas, Calzada Solidaridad entronque Paseo a la Bufa, C.P. 98000, Zacatecas, Zac. Mexico e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract.

Let π : X → C be a fibration with integral fibers over a curve C and consider a polarization H on the surface X. Let E be a stable vector bundle of rank 2 on C. We prove that the pullback π*(E) is a H-stable bundle over X. This result allows us to relate the corresponding moduli spaces of stable bundles 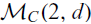$${{\mathcal M}_C}(2,d)$$ and 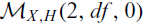$${{\mathcal M}_{X,H}}(2,df,0)$$ through an injective morphism. We study the induced morphism at the level of Brill–Noether loci to construct examples of Brill–Noether loci on fibered surfaces. Results concerning the emptiness of Brill–Noether loci follow as a consequence of a generalization of Clifford’s Theorem for rank two bundles on surfaces.

MSC classification

Primary: 14J60: Vector bundles on surfaces and higher-dimensional varieties, and their moduli
Secondary: 14D20: Algebraic moduli problems, moduli of vector bundles 14H60: Vector bundles on curves and their moduli
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 397 - 410
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author acknowledges the financial support of Programa para el Desarrollo Profesional Docente, para el Tipo Superior (PRODEP), clave UMSNH-CA-165.

References

Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of algebraic curves, Vol. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 267 (Springer-Verlag, New York, 1985), xvi+386 pp.CrossRefGoogle Scholar
Bauer, S., Parabolic bundles, elliptic surfaces and SU(2)-representation spaces of genus zero Fuchsian groups, Mathematische Annalen 290(3) (1991), 509–526.CrossRefGoogle Scholar
Coskun, I. and Huizenga, J., Brill-Noether theorems and globally generated vector bundles on Hirzebruch surfaces, Nagoya Math. J. 238 (2020), 1–36.CrossRefGoogle Scholar
Costa, L. and Miró-Roig, R. M., Brill-Noether theory for moduli spaces of sheaves on algebraic varieties, Forum Math. 22(3) (2010), 411–432.CrossRefGoogle Scholar
Costa, L. and Miró-Roig, R. M., Brill-Noether theory on Hirzebruch surfaces, J. Pure Appl. Algebra 214(9) (2010), 1612–1622.CrossRefGoogle Scholar
Friedman, R., Algebraic surfaces and holomorphic vector bundles, Universitext (Springer-Verlag, New York, 1998).CrossRefGoogle Scholar
Friedman, R., Rank two vector bundles over regular elliptic surfaces, Inventiones Mathematicae 96(2) (1989), 283–332.CrossRefGoogle Scholar
Grzegorczyk, I. and Teixidor i Bigas, M., Brill-Noether theory for stable vector bundles, in Moduli spaces and vector bundles, London Mathematical Society Lecture Note Series, vol. 359 (Cambridge University Press, Cambridge, 2009), 29–50.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer-Verlag, New York-Heidelberg, 1977).CrossRefGoogle Scholar
Huybrechts, D. and Lehn, M., The geometry of moduli spaces of sheaves, Aspects of Mathematics, vol. E31 (Friedr. Vieweg & Sohn, Braunschweig, 1997).CrossRefGoogle Scholar
Le Potier, J., Lectures on vector bundles. Translated by A. Maciocia, Cambridge Studies in Advanced Mathematics, vol. 54 (Cambridge University Press, Cambridge, 1997).Google Scholar
Maruyama, M., Stable vector bundles on an algebraic surface, Nagoya Math. J. 58 (1975), 25–68.CrossRefGoogle Scholar
Misra, S., Stable Higgs bundles on ruled surfaces, Indian J. Pure Appl Math. 51 (2020), 735–747. https://doi.org/10.1007/s13226-020-0427-3.CrossRefGoogle Scholar
Mumford, D., Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5 (Published for the Tata Institute of Fundamental Research, Bombay; Oxford University Press, London, 1970) viii+242.Google Scholar
Sundaram, N., Special divisors and vector bundles, Tohoku Math. J. (2) 39(2) (1987), 175–213.CrossRefGoogle Scholar
Teixidor i Bigas, M., Brill-Noether theory for vector bundles of rank 2, Tohoku Math. J. (2) 43(1) (1991), 123–126.CrossRefGoogle Scholar
Teixidor i Bigas, M., Rank two vector bundles with canonical determinant, Mathematische Nachrichten (2) 265 (2004).CrossRefGoogle Scholar
Teixidor i Bigas, M., Existence of vector bundles of rank two with fixed determinant and sections, Proc. Japan Acad. Ser. A Math. Sci. 86(7) (2010), 113–118.CrossRefGoogle Scholar
Takemoto, F., Stable Vector bundles on algebraic surfaces, Nagoya Math. J. 47 (1972), 29–48.CrossRefGoogle Scholar
Takemoto, F., Stable Vector bundles on algebraic surfaces II, Nagoya Math. J. 52 (1973), 173–195.CrossRefGoogle Scholar
Varma, R., On Higgs bundles on elliptic surfaces, Q. J. Math. 66(3) (2015), 991–1008.CrossRefGoogle Scholar