The Mathieu functions of integral order [1] are the solutions with period π or 2π of the equation

The eigenvalues associated with the functions ceN and seN, where N is a positive integer, denoted by aN and bN respectively, reduce to

aN = bN = N2

when q is zero. The quantities aN and bN can be expanded in powers of q, but the explicit construction of high order coefficients is very tedious. In some applications the quantity of most interest is aN – bN, which may be called the “width of the unstable zone“. It is the object of this note to derive a general formula for the leading term in the expansion of this quantity, namely

Suppose first that N is an odd integer. Then there is an expansion

where

These functions π satisfy

and

On Substituting (3) in (1), one obtains the algebraic equation

where

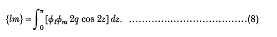
Explicitly,

{11} = q

{lm} = 0 otherwise.