No CrossRef data available.
Article contents
A note on Köthe spaces
Published online by Cambridge University Press: 18 May 2009
Extract
Let E be a locally compact space which can be expressed as the union of an increasing sequence of compact subsets Kn (n =1, 2, …) and let μ be a positive Radon measure on E. Ω is the space of equivalence classes of locally integrable functions on E. We denote the equivalence class of a function f by  and if
and if  is an equivalence class then f denotes any function belonging to f. Provided with the topology defined by the sequence of seminorms
is an equivalence class then f denotes any function belonging to f. Provided with the topology defined by the sequence of seminorms
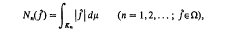
Ω is a Fréchet space. The dual of Ω is the space φ of equivalence classes of measurable, p.p. bounded functions vanishing outside a compact subset of E. For a subset Γ of Ω, the collection Λ of all  ∊Ω, such that for each g∊Γ the product fg is integrable, is called a Köthe space and Γ is said to be the denning set of Λ. The Köthe space Λx which has Λ as a denning set is called the associated Kothe space of Λ. Λ and Λx are put into duality by the bilinear form
∊Ω, such that for each g∊Γ the product fg is integrable, is called a Köthe space and Γ is said to be the denning set of Λ. The Köthe space Λx which has Λ as a denning set is called the associated Kothe space of Λ. Λ and Λx are put into duality by the bilinear form
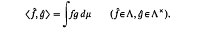
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1970


