Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T10:01:50.020Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON CHAINS AND BOUNDING PAIRS OF DEHN TWISTS

Part of: Topological manifolds Special aspects of infinite or finite groups

Published online by Cambridge University Press:  15 May 2020

FERIHE ATALAN
FERIHE ATALAN*
Affiliation:
Department of Mathematics, Atilim University, 06830Ankara, Turkey e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstarct

Let 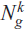$N_g^k$ be a nonorientable surface of genus g with k punctures. In the first part of this note, after introducing preliminary materials, we will give criteria for a chain of Dehn twists to bound a disc. Then, we will show that automorphisms of the mapping class groups map disc bounding chains of Dehn twists to such chains. In the second part of the note, we will introduce bounding pairs of Dehn twists and give an algebraic characterization for such pairs.

MSC classification

Primary: 20F38: Other groups related to topology or analysis
Secondary: 57N05: Topology of $E^2$, $2$-manifolds
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 1 , January 2021 , pp. 133 - 138
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Atalan, F., Outer automorphisms of mapping class groups of nonorientable surfaces, Int. J. Algebra Comput. 20(3) (2010), 437–456.CrossRefGoogle Scholar
Atalan, F. and Szepietowski, B., Automorphisms of the mapping class group of a nonorientable surface, Geom. Dedic. 189 (2017), 39–57.CrossRefGoogle Scholar
Farb, B. and Margalit, D., A primer on mapping class groups (Princeton University Press, New Jersey, 2012).Google Scholar
Hirose, S. and Kobayashi, R., A normal generating set for the Torelli group of a non-orientable closed surface, Fund. Math. 238 (2017), 29–51.CrossRefGoogle Scholar
Irmak, E. and Paris, L., Injective homomorphisms of mapping class groups of non-orientable surfaces, Geom. Dedic. 198 (2019), 149–170.CrossRefGoogle Scholar
Ivanov, N. V., Automorphisms of Teichmuller modular groups, in Lecture Notes in Mathematics, 1346 (1988), 199–270.CrossRefGoogle Scholar
Ivanov, N. V. and McCarthy, J. D., On injective homomorphisms between Teichmüller modular groups I, Invent. Math. 135 (1999), 425–486.CrossRefGoogle Scholar
Kobayashi, R., A normal generating set for the Torelli group of a compact non-orientable surface, Geom. Dedic. 195 (2018), 365–377.Google Scholar
Stukow, M., Dehn twists on nonorientable surfaces, Fund. Math. 189 (2006), 117–147.CrossRefGoogle Scholar
Vautaw, W. R., Abelian subgroups and automorphisms of the Torelli group, Ph.D. Thesis (Michigan State University, 2002), 56 pp. ISBN: 978-0493-83290-6.Google Scholar