No CrossRef data available.
Article contents
A NOTE ON A-ANNIHILATED GENERATORS OF H*QX
Published online by Cambridge University Press: 21 March 2019
Abstract
For a path connected space X, the homology algebra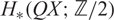 
$H_*(QX; \mathbb{Z}/2)$ is a polynomial algebra over certain generators QIx. We reinterpret a technical observation, of Curtis and Wellington, on the action of the Steenrod algebra A on the Λ algebra in our terms. We then introduce a partial order on each grading of H*QX which allows us to separate terms in a useful way when computing the action of dual Steenrod operations 
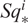$Sq^i_*$ on 
$H_*(QX; \mathbb{Z}/2)$. We use these to completely characterise the A-annihilated generators of this polynomial algebra. We then propose a construction for sequences I so that QIx is A-annihilated. As an application, we offer some results on the form of potential spherical classes in H*QX upon some stability condition under homology suspension. Our computations provide new numerical conditions in the context of hit problem.
MSC classification
Primary:
55S10: Steenrod algebra
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2019
References
Asadi-Golmankhaneh, M. A. and Eccles, P. J., Determining the characteristic numbers of self-intersection manifolds, J. Lond. Math. Soc., II. Ser. 62(1) (2000), 278–290.CrossRefGoogle Scholar
Asadi-Golmankhaneh, M. A. and Eccles, P. J., Double point self-intersection surfaces of immersions, Geom. Topol. 4, 149–170, 2000.Google Scholar
Ault, S. V. and Singer, W., On the homology of elementary Abelian groups as modules over the Steenrod algebra, J. Pure Appl. Algebra 215(12) (2011), 2847–2852.10.1016/j.jpaa.2011.04.004CrossRefGoogle Scholar
Cohen, F. R., Lada, T. J., and May, J. P.. The homology of iterated loop spaces, Lecture Notes in Mathematics, vol. 533 (Springer-Verlag, Berlin, Heidelberg, New York, 1976), vii+490.CrossRefGoogle Scholar
Curtis, E. B., The Dyer-Lashof algebra and the Λ-algebra, Ill. J. Math. 19 (1975), 231–246.CrossRefGoogle Scholar
Galatius, S., Mod p homology of the stable mapping class group, Topology 43(5) (2004), 1105–1132.CrossRefGoogle Scholar
Giambalvo, V. and Peterson, F. P.. A-generators for ideals in the Dickson algebra, J. Pure Appl. Algebra 158(2-3) (2001), 161–182.10.1016/S0022-4049(00)00051-7CrossRefGoogle Scholar
Zadeh, M. A. H. and Zare, H., An algorithmic search for A-annihilated classes in H *Q 0S 0 (in preparation).Google Scholar
Koschorke, U. and Sanderson, B., Self-intersections and higher Hopf invariants, Topology 17 (1978), 283–290.CrossRefGoogle Scholar
Kuhn, N. J., Adams filtration and generalised Hurewicz maps for infinite loop spaces, arxiv:1403.7501v1.Google Scholar
Kuhn, N. J., The mod p Hurewicz map for infinite loopspaces: theorems, examples, and conjectures. Talk at Princeton University (2015).Google Scholar
Madsen, I., On the action of the Dyer-Lashof algebra in H *(G) and H *(G/Top), PhD thesis (The University of Chicago, Ann Arbor, MI, 1970).Google Scholar
Madsen, I., On the action of the Dyer-Lashof algebra in H *(G), Pac. J. Math. 60(1) (1975), 235–275.CrossRefGoogle Scholar
May, J. P., The geometry of iterated loop spaces, Lecture Notes in Mathematics, vol. 271 (Springer-Verlag, Berlin, Heidelberg, New York, 1972), ix+175.CrossRefGoogle Scholar
Ravenel, D. C., Complex cobordism and stable homotopy groups of spheres, 2nd edition (AMS Chelsea Publishing, Providence, RI, 2004).Google Scholar
Repka, J. and Selick, P.. On the subalgebra of 
$H_*(({\mathbb R}\text {P}^\infty)^n;F_2)$ annihilated by Steenrod operations, J. Pure Appl. Algebra 127(3) (1998), 273–288.CrossRefGoogle Scholar
$H_*(({\mathbb R}\text {P}^\infty)^n;F_2)$ annihilated by Steenrod operations, J. Pure Appl. Algebra 127(3) (1998), 273–288.CrossRefGoogle ScholarSnaith, V. and Tornehave, J., On $\pi ^{{\rm S}}_\ast (B{\rm O})$ and the Arf invariant of framed manifolds, in Symposium on Algebraic Topology in honor of José Adem (Oaxtepec, 1981), Contemporary Mathematics, vol. 12 (American Mathematical Society, Providence, RI, 1982), 299–313.CrossRefGoogle Scholar
$\pi ^{{\rm S}}_\ast (B{\rm O})$ and the Arf invariant of framed manifolds, in Symposium on Algebraic Topology in honor of José Adem (Oaxtepec, 1981), Contemporary Mathematics, vol. 12 (American Mathematical Society, Providence, RI, 1982), 299–313.CrossRefGoogle ScholarSnaith, V. P., Stable homotopy around the Arf-Kervaire invariant (Birkhäuser, Basel, 2009).CrossRefGoogle Scholar
Walker, Grant and Reginald, M. W. Wood. Polynomials and the mod 2 Steenrod algebra. Vol. 1 . The Peterson hit problem, volume 441 of London Mathematical Society Lecture Note Series. Cambridge University Press, Cambridge, 2018.Google Scholar
Walker, G. and Wood, R. M. W., Polynomials and the mod 2 Steenrod algebra, vol. 2. Representations of ${\rm GL}(n,\Bbb F_2)$, London Mathematical Society Lecture Note Series, vol. 442 (Cambridge University Press, Cambridge, 2018).10.1017/9781108304092CrossRefGoogle Scholar
${\rm GL}(n,\Bbb F_2)$, London Mathematical Society Lecture Note Series, vol. 442 (Cambridge University Press, Cambridge, 2018).10.1017/9781108304092CrossRefGoogle ScholarWellington, R. J., The A-algebra H*Ωn+1∑n+1X, the Dyer-Lashof algebra, and the Λ-algebra, PhD Thesis (The University of Chicago, Ann Arbor, MI, 1977).Google Scholar
Wellington, R. J., The unstable Adams spectral sequence for free iterated loop spaces, Mem. Am. Math. Soc. 36(258) (1982), 225.Google Scholar
Wood, R. M. W., Problems in the Steenrod algebra, Bull. Lond. Math. Soc. 30(5) (1998), 449–517.10.1112/S002460939800486XCrossRefGoogle Scholar
Zare, H., The Dyer-Lashof algebra and the hit problems (submitted).Google Scholar
Zare, H., Filtered finiteness of the image of the unstable Hurewicz homomorphism with applications to bordism of immersions, Q. J. Math., hay069, https://doi.org/10.1093/qmath/hay069Google Scholar
Zare, H., On spherical classes in H *QSn, PhD Thesis (University of Manchester, 2009).Google Scholar
Zare, H., Spherical classes in some finite loop spaces of spheres, Topol. Appl. 224 (2017) 1–18.10.1016/j.topol.2017.03.013CrossRefGoogle Scholar