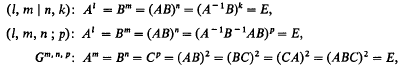Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leech, John
1962.
Some definitions of Klein's simple group of order 168 and other groups.
Proceedings of the Glasgow Mathematical Association,
Vol. 5,
Issue. 4,
p.
166.
Coxeter, H. S. M.
1962.
The Abstract Group G3, 7, 16.
Proceedings of the Edinburgh Mathematical Society,
Vol. 13,
Issue. 1,
p.
47.
Leech, John
1963.
Coset enumeration on digital computers.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 59,
Issue. 2,
p.
257.
Leech, John
1965.
Generators for certain normal subgroups of (2,3,7).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
321.
LEECH, JOHN
1970.
Computational Problems in Abstract Algebra.
p.
21.
Cannon, John J.
Dimino, Lucien A.
Havas, George
and
Watson, Jane M.
1973.
Implementation and analysis of the Todd-Coxeter algorithm.
Mathematics of Computation,
Vol. 27,
Issue. 123,
p.
463.
Conder, Marston
1990.
Hurwitz groups: A brief survey.
Bulletin of the American Mathematical Society,
Vol. 23,
Issue. 2,
p.
359.
Campbell, C. M.
Conder, M. D. E.
and
Robertson, E. F.
1994.
Defining-relations for Hurwitz groups.
Glasgow Mathematical Journal,
Vol. 36,
Issue. 3,
p.
363.
Edjvet, M.
and
Juhász, A.
2008.
The groups Gm,n,p.
Journal of Algebra,
Vol. 319,
Issue. 1,
p.
248.
Mushtaq, Qaiser
and
Mumtaz, Nighat
2018.
$$PSL\left( 2,7\right) $$
P
S
L
2
,
7
and carbon allotrope D168 Schwarzite.
Journal of Mathematical Chemistry,
Vol. 56,
Issue. 8,
p.
2485.