Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T20:20:54.594Z Has data issue: false hasContentIssue false
  • English
  • Français

NORMALLY ORDERED SEMIGROUPS

Published online by Cambridge University Press:  01 May 2008

VÍTOR H. FERNANDES
VÍTOR H. FERNANDES*
Affiliation:
Departamento de Matemática, F.C.T., Universidade Nova de Lisboa, 2829-516 Monte da Caparica, Portugal; also: Centro de Álgebra, Universidade de Lisboa, Av. Prof. Gama Pinto 2, 1649-003 Lisboa, Portugal; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we introduce the notion of normally ordered block-group as a natural extension of the notion of normally ordered inverse semigroup considered previously by the author. We prove that the class NOS of all normally ordered block-groups forms a pseudovariety of semigroups and, by using the Munn representation of a block-group, we deduce the decompositions in Mal'cev products NOS = EI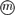POI and NOS ∩ A = N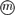POI, where A, EI and N denote the pseudovarieties of all aperiodic semigroups, all semigroups with just one idempotent and all nilpotent semigroups, respectively, and POI denotes the pseudovariety of semigroups generated by all semigroups of injective order-preserving partial transformations on a finite chain. These relations are obtained after showing the equalities BG = EI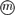Ecom = N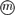Ecom, where BG and Ecom denote the pseudovarieties of all block-groups and all semigroups with commuting idempotents, respectively.

Keywords

20M0720M1820M20
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 50 , Issue 2 , May 2008 , pp. 325 - 333
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Almeida, J.Finite semigroups and universal algebra (World Scientific, Singapore, 1995).CrossRefGoogle Scholar
2.Almeida, J. and Volkov, M. V.The gap between partial and full, Int. J. Algebra Comput. 8 (1998), 399–430.CrossRefGoogle Scholar
3.Cowan, D. F. and Reilly, N. R.Partial cross-sections of symmetric inverse semigroups, Int. J. Algebra Comput. 5 (1995), 259–287.CrossRefGoogle Scholar
4.Easdown, D.The minimal faithful degree of a fundamental inverse semigroup, Bull. Austral. Math. Soc. 35 (1987), 373–378.CrossRefGoogle Scholar
5.Fernandes, V. H.Semigroups of order-preserving mappings on a finite chain: a new class of divisors, Semigroup Forum 54 (1997), 230–236.CrossRefGoogle Scholar
6.Fernandes, V. H.Normally ordered inverse semigroups, Semigroup Forum 58 (1998), 418–433.CrossRefGoogle Scholar
7.Fernandes, V. H., A new class of divisors of semigroups of isotone mappings of finite chains, Russ. Math 46 (2002), 47–55 [translation of Izvestiya VUZ. Matematika 3 (478) (2002), 51–59] (English, Russian).Google Scholar
8.Fernandes, V. H., The idempotent-separating degree of a block-group, Semigroup Forum, to appear.Google Scholar
9.Fremlin, D. H. and Higgins, P. M., Deciding some embeddability problems for semigroups of mappings, in Semigroups (eds. Smith, Paula et al. ), (World Scientific, 2000), 87–95.CrossRefGoogle Scholar
10.Henckell, K., Margolis, S., Pin, J-E. and Rhodes, J., Ash's type II theorem, profinite topology and Malcev products. Part I, Int. J. Algebra Comput. 1 (1991), 411–436.CrossRefGoogle Scholar
11.Higgins, P. M.Divisors of semigroups of order-preserving mappings on a finite chain, Int. J. Algebra Comput. 5 (1995), 725–742.CrossRefGoogle Scholar
12.Howie, J. M.Fundamentals of semigroup theory (Oxford University Press, 1995).CrossRefGoogle Scholar
13.Petrich, M.Inverse semigroups (John Wiley & Sons, 1984).Google Scholar
14.Pin, J.-E., Varieties of formal languages, (North Oxford Academic, 1986).CrossRefGoogle Scholar
15.Pin, J.-E., BG=PG: a success story, in Semigroups, formal languages and groups, ed. Fountain, J., (Kluwer Academic Publisher, 1995), 33–47.CrossRefGoogle Scholar
16.Repnitskĭ, V. B. and Volkov, M. V., The finite basis problem for the pseudovariety O, Proc. Roy. Soc. Edinburgh, Sect. A, 128 (1998), 661–669.CrossRefGoogle Scholar
17.Rhodes, J. and Weil, P.Decomposition techniques for finite semigroups, using categories I, J. Pure Appl. Algebra 62 (1989), 269–284.CrossRefGoogle Scholar
18.Vernitskii, A. and Volkov, M. V., A proof and generalisation of Higgins' division theorem for semigroups of order-preserving mappings, Izv.vuzov. Matematika 1 (1995), 38–44.Google Scholar