Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ferenbaugh, Charles R.
1993.
The Genus-zero problem for n|h-type groups.
Duke Mathematical Journal,
Vol. 72,
Issue. 1,
Heon Kim, Chang
and
Kyung Koo, Ja
2000.
The normalizer of γ1(N) in psl2(R).
Communications in Algebra,
Vol. 28,
Issue. 11,
p.
5303.
Lang, Mong-Lung
2001.
Normalizers of the Congruence Subgroups of the Hecke Groups G4 and G6.
Journal of Number Theory,
Vol. 90,
Issue. 1,
p.
31.
Lang, Mong Lung
2004.
Groups commensurable with the modular group.
Journal of Algebra,
Vol. 274,
Issue. 2,
p.
804.
Chua, Kok Seng
and
Lang, Mong Lung
2004.
Congruence Subgroups Associated to the Monster.
Experimental Mathematics,
Vol. 13,
Issue. 3,
p.
343.
Lang, Mong Lung
2007.
The structure of the normalisers of the congruence subgroups of the Hecke groupG5.
Bulletin of the London Mathematical Society,
Vol. 39,
Issue. 1,
p.
53.
Güler, Bahadır Özgür
Kör, Tuncay
and
Şanlı, Zeynep
2016.
Solutions to some congruence equations via suborbital graphs.
SpringerPlus,
Vol. 5,
Issue. 1,
Zemel, Shaul
2017.
Normalizers of congruence groups in SL2(ℝ) and automorphisms of lattices.
International Journal of Number Theory,
Vol. 13,
Issue. 05,
p.
1275.
Kader, Serkan
2017.
Circuits in Suborbital Graphs for The Normalizer.
Graphs and Combinatorics,
Vol. 33,
Issue. 6,
p.
1531.
Im, Bo-Hae
Jeon, Daeyeol
and
Kim, Chang Heon
2017.
Normalizers of intermediate congruence subgroups of the Hecke subgroups.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
787.
Paulhus, Jennifer
and
Rojas, Anita M.
2017.
Completely Decomposable Jacobian Varieties in New Genera.
Experimental Mathematics,
Vol. 26,
Issue. 4,
p.
430.
Yazıcı Gözütok, Nazlı
and
Güler, Bahadır Özgür
2019.
Suborbital Graphs for the Group $$\Gamma _{C}(N)$$ Γ C ( N ).
Bulletin of the Iranian Mathematical Society,
Vol. 45,
Issue. 2,
p.
593.
Yazıcı Gözütok, Nazlı
Gözütok, Uğur
and
Güler, Bahadır Özgür
2019.
Maps Corresponding to the Subgroups $$\varGamma _0(N)$$ of the Modular Group.
Graphs and Combinatorics,
Vol. 35,
Issue. 6,
p.
1695.
Şanlı, Zeynep
Köroğlu, Tuncay
and
Güler, Bahadır Özgür
2019.
The normalizer of .
Mathematical Methods in the Applied Sciences,
Vol. 42,
Issue. 16,
p.
5403.
Yazıcı Gözütok, Nazlı
and
Güler, Bahadır Özgür
2022.
Quadrilateral and Hexagonal Maps Corresponding to the Subgroups $$\Gamma _0(N)$$ of the Modular Group.
Graphs and Combinatorics,
Vol. 38,
Issue. 3,
Dose, Valerio
Lido, Guido
and
Mercuri, Pietro
2022.
Automorphisms of Cartan modular curves of prime and composite level.
Algebra & Number Theory,
Vol. 16,
Issue. 6,
p.
1423.
Murakami, Yuya
2023.
Hurwitz class numbers with level and modular correspondences.
Research in Number Theory,
Vol. 9,
Issue. 2,


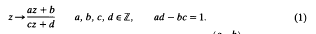
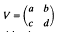 remembering that
remembering that 
