Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-06T13:12:34.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal curvature of minimal submanifolds in a sphere

Published online by Cambridge University Press:  18 May 2009

Sharief Deshmukh
Sharief Deshmukh
Affiliation:
Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh-11451, Saudi Arabia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Simons [5] has proved a pinching theorem for compact minimal submanifolds in a unit sphere, which led to an intrinsic rigidity result. Sakaki [4] improved this result of Simons for arbitrary codimension and has proved that if the scalar curvature S of the minimal submanifold Mn of Sn+P satisfies

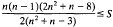
then either Mn is totally geodesic or S= 2/3 in which case n = 2 and M2 is the Veronese surface in a totally geodesic 4-sphere. This result of Sakaki was further improved by Shen [6] but only for dimension n=3, where it is shown that if S>4, then M3 is totally geodesic (cf. Theorem 3, p. 791).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 1 , January 1997 , pp. 29 - 33
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Barbosa, J. L. and do Carmo, M., Stability of minimal surfaces and eigenvalues of the Laplacian, Math. Z. 173 (1980), 13–28.CrossRefGoogle Scholar
2.Cheng, S.-Y., Eigenvalue comparison theorems and its geometric applications, Math. Z. 143 (1975), 289–297.Google Scholar
3.Chern, S. S., do Carmo, M. and Kobayashi, S., Minimal submanifolds of a sphere with second fundamental form of constant length, Functional analysis and related fields (Springer, 1970), 59–75.Google Scholar
4.Sakaki, M., Remarks on the rigidity and stability of minimal submanifolds, Proc. Amer. Math. Soc. 106 (1989), 793–795.CrossRefGoogle Scholar
5.Simons, J., Minimal varieties in riemannian manifolds, Ann. of Math. (2) 88 (1968), 62–105.Google Scholar
6.Shen, Y. B., Curvature pinching for the three-dimensional minimal submanifolds in a sphere, Proc. Amer. Math. Soc. 115 (1992), 791–795.CrossRefGoogle Scholar