Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T20:30:26.786Z Has data issue: false hasContentIssue false
  • English
  • Français

NONBINARY DELSARTE–GOETHALS CODES AND FINITE SEMIFIELDS

Part of: Finite fields and commutative rings (number-theoretic aspects) Other nonassociative rings and algebras Forms and linear algebraic groups

Published online by Cambridge University Press:  07 May 2020

IGNACIO F. RÚA Open the ORCID record for IGNACIO F. RÚA [Opens in a new window]
IGNACIO F. RÚA*
Affiliation:
Departamento de Matemáticas, Universidad de Oviedo, Oviedo, Spain, e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Symplectic finite semifields can be used to construct nonlinear binary codes of Kerdock type (i.e., with the same parameters of the Kerdock codes, a subclass of Delsarte–Goethals codes). In this paper, we introduce nonbinary Delsarte–Goethals codes of parameters 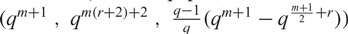$(q^{m+1}\ ,\ q^{m(r+2)+2}\ ,\ {\frac{q-1}{q}(q^{m+1}-q^{\frac{m+1}{2}+r})})$ over a Galois field of order 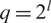$q=2^l$ , for all 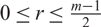$0\le r\le\frac{m-1}{2}$ , with m ≥ 3 odd, and show the connection of this construction to finite semifields.

MSC classification

Primary: 11T71: Algebraic coding theory; cryptography 11E08: Quadratic forms over local rings and fields
Secondary: 17D99: None of the above, but in this section
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Special Issue S1: Workshop on Nonassociative algebras and their applications , December 2020 , pp. S186 - S205
Copyright
© The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bini, G. and Flamini, F., Finite commutative rings and their applications (Kluwer Academic Publishers, Boston, MA, 2002).Google Scholar
Boztaş, S., Hammons, R. and Kumar, P.V., 4-phase sequences with near-optimum correlation properties, IEEE Trans. Inform. Theory IT-38(3) (1992), 1101–1113.CrossRefGoogle Scholar
Brown, E. H., Generalizations of the Kervaire invariant, Ann. Math. 95(2) (1972), 368–383.CrossRefGoogle Scholar
Calderbank, A. R., Cameron, P. J., Kantor, W. M. and Seidel, J. J., ${\mathbb{Z}_4}$ -Kerdock codes, orthogonal spreads, and extremal Euclidean line-sets, Proc. London Math. Soc. 75 (1997), 436–480.CrossRefGoogle Scholar
Carlet, C., $\mathbb{Z}_{2^k}$ -linear codes, IEEE Trans. Inform. Theory 44(4) (1998) 1543–1547.CrossRefGoogle Scholar
Delsarte, Ph., Bilinear forms over a finite field, with applications to coding theory, J. Comb. Theory Ser. A 25 (1978), 226–241.CrossRefGoogle Scholar
Delsarte, P. and Goethals, J.-M., Alternating bilinear forms over GF(q), J. Comb Theory Ser. A 19(1) (1975), 26–50.CrossRefGoogle Scholar
González, S., Martínez, C. and Rúa, I. F., Symplectic spread based generalized Kerdock codes, Des. Codes Cryptogr. 42(2) (2007), 213–226.CrossRefGoogle Scholar
Hammons, A. R. Jr., Kumar, P. V., Calderbank, A. R., Sloane, N. J. A. and Sole, P., The ${\mathbb{Z}_4}$ -linearity of Kerdock, Preparata, Goethals and related codes, IEEE Trans. Inform. Theory 40 (1994), 301–319.CrossRefGoogle Scholar
Hirschfeld, J. W. P., Projective geometries over finite fields (Oxford Science Publications, New-York, 1979).Google Scholar
Kantor, W. M., Spreads, translation planes and Kerdock sets. I., SIAM J. Algebraic Discrete Methods 3 (1982), 151–165.CrossRefGoogle Scholar
Kantor, W. M., Commutative semifields and symplectic spreads, J. Algebra 270 (2003), 96–114.Google Scholar
Kerdock, A. M., A class of low-rate non-linear binary codes, Inform. Control 20 (1972), 182–187.CrossRefGoogle Scholar
Klapper, A., Cross-correlations of geometric sequences in characteristic two, Des. Codes Cryptogr. 3 (1993) 347–377.CrossRefGoogle Scholar
Kumar, P. V., Helleseth, T., Calderbank, A. R. and Hammons, A. R. Jr., Large families of quaternary sequences with low correlation, IEEE Trans. Inform. Theory 42 (1996), 579–592.CrossRefGoogle Scholar
Kumar, P. V., Francis Lu, H. F., Helleseth, T. and Shin, D.-J., On the large family of low correlation quaternary sequences S(2), in IEEE International Conference on Personal Wireless Communications (ICPWC 2000), Hyderbad, December 17–20, 2000.Google Scholar
Kurakin, V. L., Kuzmin, A. S., Markov, V. T., Mikhalev, A. V. and Nechaev, A. A., Linear codes and polylinear recurrences over finite rings and modules (a survey), in Applied Algebra, Algebraic Algorithms and Error-Correcting Codes 13, Lecture Notes in Computer Science, vol. 1719 (Springer, Berlin, 1999), 363–391.Google Scholar
Kuzmin, A. S. and Nechaev, A. A., Linearly presented codes and Kerdock code over an arbitrary Galois field of the characteristic 2, Russ. Math. Surv. 49(5) (1994), 183–184.CrossRefGoogle Scholar
Kuzmin, A. S. and Nechaev, A. A., ${\mathbb{Z}_4}$ -linearity, two approaches, in Fifth International Workshop on Algebraic and Combinatorial Coding Theory, Proceedings, Sozopol, Bulgaria, (1996), 212–215.Google Scholar
Kuzmin, A. S., Markov, V. T., Nechaev, A. A. and Neljubin, A. S. A generalization of the binary Preparata code, Discrete Appl. Math. 154 (2006), 337–345.CrossRefGoogle Scholar
Lidl, R. and Niederreiter, H., Finite Fields, in Encyclopedia of mathematics and its applications Rota, (G.-C., Editor), vol. 20, (Addison-Wesley, Cambridge (UK), 1983).Google Scholar
López-D az, M. C. and Rúa, I. F., An invariant for quadratic forms valued in Galois rings of characteristic 4, Finite Fields Appl. 13(4) (2007), 946–961.CrossRefGoogle Scholar
MacWilliams, F. J. and Sloane, N. J. A., The theory of error-correcting codes (North-Holland, Amsterdam, 1977).Google Scholar
McDonald, B. R., Finite rings with identity, in Pure and applied mathematics (Taft, E. J., Editor), vol. 28 (Marcel Dekker, New York, 1974).Google Scholar
Mullen, G. L. and Panario, D., Handbook of finite fields (CRC-Press, Boca-Raton 2013).CrossRefGoogle Scholar
Muller, D. E., Application of Boolean algebra to switching circuit design and to error detection, IRE Trans. Comput. 3 (1954), 6–12.Google Scholar
Nechaev, A. A., Trace function in Galois ring and noise stable codes, in V All-Union Symposium on Theory of Rings, Algebras and Modules, Novosibirsk (1982), 97.Google Scholar
Nechaev, A. A., Kerdock’s code in a cyclic form, Diskret. Mat.1 (1989), 123–139.Google Scholar
Nechaev, A. A. and Kuzmin, A. S., Trace-function on a Galois ring in coding theory, in AAECC 1997, Lecture Notes in Computer Science, vol. 1255 (Springer, Berlin, Heidelberg, 1997), 277–290.Google Scholar
Preparata, F. P., A class of optimum non-linear double-error correcting codes, Inform. Control 13 (1968) 378–400.CrossRefGoogle Scholar
Reed, I. S., A class of multiple-error-correcting codes and the decoding scheme, IEEE Trans. Inf. Theory 4 (1954), 38–49.Google Scholar
Roman, S., Advanced linear algebra, graduate texts in mathematics, vol. 135 (Springer-Verlag, New York, 1992)CrossRefGoogle Scholar
Schmidt, K.-U., ${\mathbb{Z}_4}$ -valued quadratic forms and quaternary sequence families, IEEE Trans. Inf. Theory 55(12) (2009), 5803–5810.Google Scholar
Schmidt, K.-U., Symmetric bilinear forms over finite fields of even characteristic, J. Comb. Theory Ser. A 117 (2010), 1011–1026.CrossRefGoogle Scholar
Sheekey, J., Binary additive MRD codes with minimum distance n − 1 must contain a semifield spread set. Des. Codes Cryptogr. 87 (2019), 2571–2583.CrossRefGoogle Scholar