Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-28T23:47:20.074Z Has data issue: false hasContentIssue false
  • English
  • Français

A new class of Hadamard matrices

Published online by Cambridge University Press:  18 May 2009

E. Spence
E. Spence
Affiliation:
University of GlasgowGlasgow, W.2
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Hadamard matrix H is an orthogonal square matrix of order m all the entries of which are either + 1 or - 1; i. e.

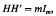
where H′ denotes the transpose of H and Im is the identity matrix of order m. For such a matrix to exist it is necessary [1] that

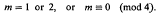
It has been conjectured, but not yet proved, that this condition is also sufficient. However, many values of m have been found for which a Hadamard matrix of order m can be constructed. The following is a list of such m (p denotes an odd prime).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 8 , Issue 1 , January 1967 , pp. 59 - 62
Copyright
Copyright © Glasgow Mathematical Journal Trust 1967

References

1.Paley, R. E. A. C., On orthogonal matrices, J. Math. Phys. 12 (1933), 311–320.CrossRefGoogle Scholar
2.Williamson, J., Hadamard's determinant theorem and the sum of four squares, Duke Math. J. 11 (1944), 65–81.CrossRefGoogle Scholar
3.Williamson, J., Note on Hadamard's determinant theorem, Bull. Amer. Math. Soc. 53 (1947), 608–613.CrossRefGoogle Scholar
4.Baumert, L., Golomb, S. W. and Hall, Marshall Jr, Discovery of an Hadamard matrix of order 92, Bull. Amer. Math. Soc. 68 (1962), 237–238.CrossRefGoogle Scholar
5.Baumert, L. D. and Hall, Marshall Jr, Hadamard matrices of the Williamson type, Math. Comp. 10 (1965), 442–447.Google Scholar
6.Goldberg, K., Hadamard matrices of order cube plus one, Proc. Amer. Math. Soc. 17 (1966), 744–746.Google Scholar
7.Baumert, L. D., Hadamard matrices of orders 116 and 232, Bull. Amer. Math. Soc. 72 (1966), 237.CrossRefGoogle Scholar
8.Ehlich, H., Neue Hadamard-Matrizen, Arch. Math. 16 (1965), 34–36.CrossRefGoogle Scholar
9.Singer, J., A Theorem in finite projective geometry and some applications to number theory, Trans. Amer. Math. Soc. 43 (1938), 377–385.CrossRefGoogle Scholar
10.Ryser, H. J., Combinatorial mathematics, Cams Mathematical Monographs No. 14, 1963.Google Scholar
11.Brauer, A., On a new class of Hadamard determinants, Math. Z. 58 (1953), 219–225.CrossRefGoogle Scholar