Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T02:56:05.649Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MOMENTS OF MINKOWSKI QUESTION MARK FUNCTION: THE DYADIC PERIOD FUNCTION

Published online by Cambridge University Press:  30 July 2009

GIEDRIUS ALKAUSKAS
GIEDRIUS ALKAUSKAS*
Affiliation:
The Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius, Lithuania and School of Mathematical Sciences, University of Nottingham, University Park, Nottingham NG7 2RD, UK e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Minkowski question mark function ?(x) arises as a real distribution of rationals in the Farey tree. We examine the generating function of moments of ?(x). It appears that the generating function is a direct dyadic analogue of period functions for Maass wave forms and it is defined in the cut plane 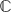\ (1, ∞). The exponential generating function satisfies an integral equation with kernel being the Bessel function. The solution of this integral equation leads to the definition of dyadic eigenfunctions, arising from a certain Hilbert–Schmidt operator. Finally, we describe p-adic distribution of rationals in the Stern–Brocot tree. Surprisingly, the Eisenstein series G2(z) does manifest in both real and p-adic cases.

Keywords

Primary – 11A5526A3011F03Secondary – 33C10
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 1 , January 2010 , pp. 41 - 64
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Alkauskas, G., An asymptotic formula for the moments of Minkowski question mark function in the interval [0, 1], Lith. Math. J. 48 (4) (2008), 357–367.CrossRefGoogle Scholar
2.Alkauskas, G., Generating and zeta functions, structure, spectral and analytic properties of the moments of the Minkowski question mark function, Involve 2 (2) (2009), 121–159.Google Scholar
3.Alkauskas, G., The Minkowski question mark function: Explicit series for the dyadic period function and moments, Math. Comp. Available at http://www.ams.org/mcom/0000-000-00/S0025-5718-09-02263-7/home.html.Google Scholar
4.Bonanno, C., Graffi, S. and Isola, S., Spectral analysis of transfer operators associated to Farey fractions, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 19 (1) (2008), 1–23.Google Scholar
5.Bonanno, C. and Isola, S., Orderings of the rationals and dynamical systems, Colloq. Math. 116 (2009), 165–189.Google Scholar
6.Calkin, N. and Wilf, H., Recounting the rationals, Amer. Math. Mon. 107 (2000), 360–363.CrossRefGoogle Scholar
7.Cassels, J. W. S. and Fröhlich, A. (eds.), Algebraic number theory (Academic Press, London, 1967).Google Scholar
8.Conway, J. H., On numbers and games (A K Peters Ltd., Natick, MA, 2001) 82–86.Google Scholar
9.Denjoy, A., Sur une fonction réelle de Minkowski, J. Math. Pures Appl. 17 (1938), 105–151.Google Scholar
10.Dilcher, K. and Stolarsky, K. B., A polynomial analogue to the Stern sequence, Int. J. Number Theory 3 (1) (2007), 85–103.Google Scholar
11.Dushistova, A. and Moshchevitin, N. G., On the derivative of the Minkowski question mark funtion ?(x), arXiv:0706.2219.Google Scholar
12.Esposti, M. D., Isola, S. and Knauf, A., Generalized Farey trees, transfer operators and phase transitions, Comm. Math. Phys. 275 (2) (2007), 297–329.CrossRefGoogle Scholar
13.Finch, S. R., Mathematical constants (Cambridge University Press, Cambridge, UK, 2003), 441–443, 151–154.Google Scholar
14.Girgensohn, R., Constructing singular functions via Farey fractions, J. Math. Anal. Appl. 203 (1996), 127–141.Google Scholar
15.Grabner, P. J., Kirschenhofer, P. and Tichy, R. F., Combinatorial and arithmetical properties of linear numeration systems, Combinatorica 22 (2) (2002), 245–267.CrossRefGoogle Scholar
16.Isola, S., On the spectrum of Farey and Gauss maps, Nonlinearity 15 (2002), 1521–1539.CrossRefGoogle Scholar
17.Karlin, S., A first course in stochastic processes (Academic Press, New York and London, 1968).Google Scholar
18.Kesseböhmer, M. and Stratmann, B. O., A multifractal analysis for Stern–Brocot intervals, continued fractions and Diophantine growth rates, J. Reine Angew. Math. 605 (2007), 133–163.Google Scholar
19.Kesseböhmer, M. and Stratmann, B. O., Fractal analysis for sets of non-differentiability of Minkowski's question mark function, J. Number Theory 128 (2008), 2663–2686.CrossRefGoogle Scholar
20.Khinchin, A. Ya., Continued fractions (The University of Chicago Press, Chicago and London, 1964).Google Scholar
21.Kinney, J. R., Note on a singular function of Minkowski, Proc. Amer. Math. Soc. 11 (5) (1960), 788–794.Google Scholar
22.Kolmogorov, A. N. and Fomin, S. V., Elements of the theory of functions and functional analysis (Nauka, Moscow, 1989). Available at http://www.ams.org/mathscinet-getitem?mr=1025126.Google Scholar
23.Lagarias, J. C., Number theory and dynamical systems, in The unreasonable effectiveness of number theory (Orono, ME, 1991), Amer. Math. Soc., Proc. Sympos. Appl. Math. 46 (1992), 35–72.CrossRefGoogle Scholar
24.Lagarias, J. C. and Tresser, C. P., A walk along the branches of the extended Farey tree, IBM J. Res. Develop. 39 (3) (1995), 788–794.CrossRefGoogle Scholar
25.Lamberger, M., On a family of singular measures related to Minkowski's ?(x) function, Indag. Math. N.S. 17 (1) (2006), 45–63.CrossRefGoogle Scholar
26.Lavrentjev, M. A. and Shabat, B. V., Methods in the theory of functions of complex variable (Nauka, Moscow, 1987).Google Scholar
27.Lewis, J. B., Spaces of holomorphic functions equivalent to the even Maass cusp forms, Invent. Math. 127 (2) (1997), 271–306.Google Scholar
28.Lewis, J. B. and Zagier, D., Period functions for Maass wave forms. I, Ann. Math. (2), 153 (1) (2001), 191–258.Google Scholar
29.Minkowski, H., Zur Geometrie der Zahlen, Verhandlungen des III Internationalen Mathematiker-Kongresous (Heidelberg 1904), 164–173. [Also: Werke, vol. II, 43–52.].Google Scholar
30.Newman, M., Recounting the rationals, Amer. Math. Mon. 110 (2003), 642–643.Google Scholar
31.Okamoto, H. and Wunsch, M., A geometric construction of continuous, strictly increasing singular functions, Proc. Japan Acad. 83 Ser. A (2007), 114–118.Google Scholar
32.Panti, G., Multidimensional continued fractions and a Minkowski function, Monatsh. Math. 154 (3) (2008), 247–264.CrossRefGoogle Scholar
33.Paradís, J., Viader, P. and Bibiloni, L., A new light on Minkowski's ?(x) function, J. Number Theory 73 (2) (1998), 212–227.Google Scholar
34.Paradís, J., Viader, P. and Bibiloni, L., The derivative of Minkowski's ?(x) function, J. Math. Anal. Appl. 253 (1) (2001), 107–125.Google Scholar
35.Ramharter, G., On Minkowski's singular function, Proc. AMS 99 (3), (1987), 596–597.Google Scholar
36.Reese, S., Some Fourier–Stieltjes coefficients revisited, Proc. Amer. Math. Soc. 105 (2) (1989), 384–386.Google Scholar
37.Ryde, F., On the relation between two Minkowski functions, J. Number Theory 77 (1983), 47–51.CrossRefGoogle Scholar
38.Salem, R., On some singular monotonic functions which are strictly increasing, Trans. Amer. Math. Soc. 53 (3) (1943), 427–439.CrossRefGoogle Scholar
39.Serre, J.-P., A course in arithmetic, in Graduate texts in mathematics (Springer, New York and Heidelberg, 1996).Google Scholar
40.Sloane, N., The On-line Encyclopedia of integer sequences. Available at http://www.research.att.com/~njas/sequences/Google Scholar
41.Stern, M. A., Über eine zahlentheoretische Funktion, J. Reine Angew. Math. 55 (1858), 193–220.Google Scholar
42.Tichy, R. F., Uitz, J., An extension of Minkowski's singular function, Appl. Math. Lett. 8 (5) (1995), 39–46.CrossRefGoogle Scholar
43.Watson, G. N., A treatise on the theory of Bessel functions, 2nd ed. (Cambridge University Press, Cambridge, UK, 1996).Google Scholar
44.Wirsing, E., On the theorem of Gauss–Kuzmin–Lévy and a Frobenius-type theorem for function spaces, Acta Arith. 24 (1973/74), 507–528.CrossRefGoogle Scholar
45.Wirsing, E., Jörn Steuding's Problem, Palanga 2006 (preprint).Google Scholar
46.Zagier, D., New points of view on the Selberg zeta function (preprint).Google Scholar