Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T08:24:39.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal line graphs

Published online by Cambridge University Press:  18 May 2009

David P. Sumner
David P. Sumner
Affiliation:
University of South CarolinaColumbia South Carolina 29208, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper all graphs will be ordinary graphs, i.e. finite, undirected, and without loops or multiple edges. For points x and y of a graph G, we shall indicate that x is adjacent to y by writing x ⊥ y, and if x is not adjacent to y we shall write x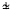y. We shall denote the degree of a point x by δ(x) and the minimal degree of G by δ(G).

By the line graph of a graph G we shall mean the graph L(G) whose points are the edges of G, with two points of L(G) adjacent whenever they are adjacent in G. A graph G is said to be a line graph if there exists a graph H such that G = L(H).

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 1 , January 1976 , pp. 12 - 16
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Beineke, L. W., Characterizations of derived graphs, j. Comb. Theory 9 (1970), 129–135.CrossRefGoogle Scholar
2.Harary, F., Graph Theory (Reading, Massachusetts: Addison-Wesley Publishing Company, 1969).CrossRefGoogle Scholar
3.Krauz, J., Démonstration nouvelle d'un théoréme de Whitney sur les réseaux, Mat. Fiz. Lapok 50 (1943), 75–89.Google Scholar
4.van Rooij, A. and Wilf, H., The interchange graphs of a finite graph, Ada Math. Acad. Sci. Hungar. 16 (1965), 263–269.CrossRefGoogle Scholar