Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T20:47:58.264Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurable majorants in L1

Published online by Cambridge University Press:  18 May 2009

Alan Lambert
Alan Lambert
Affiliation:
Department of Mathematics, University of North Carolina, Charlotte, North Carolina 28223, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

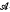Given a probability space (X, ℱ, μ) and a σ-algebra A ⊂ ℱ, arguably the most powerful tool in gaining information about an ℱ-measurable function f from restricted knowledge of -measurability is that of the conditional expectation 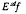E(f | ); written throughout the remainder of this note. Two properties of conditional expectation that may be exploited to gain information, but which also limit conditional expectation's use are the following.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 2 , May 1997 , pp. 183 - 192
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Akermann, C. and Weaver, N., Minimal upper bounds of commuting operators, preprint.Google Scholar
2.Douglas, R., Contractive projections on Lrspace, Pacific J. Math., 15 (1965), 443–462.CrossRefGoogle Scholar
3.Dodds, P., Huijsmans, C., and DePagter, B., Characterizations of conditional expectation-type operators, Pacific J. Math., 141 No. 1 (1990), 55–77.CrossRefGoogle Scholar
4.Foguel, S., The ergodic theory of Markov processes (Van Nostrand, 1969).Google Scholar
5.Lambert, A., L p multipliers and nested sigma-algebras, to appear in Advances in Operator Theory.Google Scholar
6.Moy, S., Characterizations of conditional expectations as a transformation on function spaces, Pacific J. Math., 4 (1954), 47–64.CrossRefGoogle Scholar