Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bourhim, A.
Mashreghi, J.
and
Stepanyan, A.
2014.
Nonlinear maps preserving the minimum and surjectivity moduli.
Linear Algebra and its Applications,
Vol. 463,
Issue. ,
p.
171.
Bourhim, Abdellatif
and
Lee, Ji Eun
2018.
Multiplicatively local spectrum-preserving maps.
Linear Algebra and its Applications,
Vol. 549,
Issue. ,
p.
291.
Abdelali, Zine El Abidine
and
Bourhim, Abdellatif
2018.
Maps preserving the local spectrum of quadratic products of matrices.
Acta Scientiarum Mathematicarum,
Vol. 84,
Issue. 1-2,
p.
49.
Sadeghi, Hossein
and
Mirzapour, Farzollah
2018.
Peripheral Local Spectrum Preservers of Jordan Products of Operators.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 2,
p.
437.
Abdelali, Z.
Bourhim, A.
and
Mabrouk, M.
2018.
Lie product and local spectrum preservers.
Linear Algebra and its Applications,
Vol. 553,
Issue. ,
p.
328.
Abdelali, Zine El Abidine
Achchi, Abdelali
and
Marzouki, Rabi
2019.
Maps preserving the local spectral radius zero of generalized product of operators.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 10,
p.
2021.
Achchi, Abdelali
2019.
Maps preserving the inner local spectral radius zero of generalized product of operators.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 68,
Issue. 2,
p.
355.
Bourhim, Abdellatif
and
Costara, Constantin
2019.
Linear Maps Preserving Matrices of Local Spectral Radius Zero at a Fixed Vector.
Canadian Journal of Mathematics,
Vol. 71,
Issue. 4,
p.
749.
Benbouziane, Hassane
Ech-Chérif Elkettani, Mustapha
and
Herrou, Imane
2019.
Local spectral subspace preservers.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 68,
Issue. 2,
p.
293.
Abdelali, Zine El Abidine
and
Nkhaylia, Hamid
2019.
Maps preserving the pseudo spectrum of skew triple product of operators.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 11,
p.
2297.
Abdelali, Zine El Abidine
and
Nkhaylia, Hamid
2020.
Condition Spectrum of Rank One Operators and Preservers of the Condition Spectrum of Skew Product of Operators.
Complex Analysis and Operator Theory,
Vol. 14,
Issue. 7,
Yan, Kai
Zeng, Qingping
and
Zhu, Yucan
2020.
On Drazin Spectral Equation for the Operator Products.
Complex Analysis and Operator Theory,
Vol. 14,
Issue. 1,
Abdelali, Zine El Abidine
and
Aharmim, Bouchra
2021.
Multiplicatively spectrum preserving maps on rectangular matrices.
Linear and Multilinear Algebra,
Vol. 69,
Issue. 16,
p.
3099.
Bouramdane, Y.
and
Ech-Chérif El Kettani, M.
2022.
Maps preserving some spectral domains of skew products of operators.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 21,
p.
6978.
Hajighasemi, Sepide
and
Hejazian, Shirin
2022.
Maps preserving some spectral domains of operator products.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 12,
p.
2367.
Benbouziane, Hassane
Daoudi, Aukacha
Kettani, Mustapha Ech-Chérif El
and
El Khchin, Ismail
2023.
Maps Preserving the $$\partial $$-Spectrum of Product or Triple Product of Operators.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 6,
Wang, Ying
2023.
Some spectral domain in approximate point-spectrum-preserving maps on $\mathcal {B}(\mathcal {X})$.
Journal of Inequalities and Applications,
Vol. 2023,
Issue. 1,
Elhodaibi, Mhamed
and
Saber, Somaya
2023.
Maps preserving some spectral domains of Jordan product of operators.
Acta Scientiarum Mathematicarum,
Vol. 89,
Issue. 3-4,
p.
621.
Marzouki, Rabi
and
Saber, Somaya
2024.
Preservers of the local spectral radii.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 73,
Issue. 3,
p.
1073.
Bourhim, Abdellatif
and
Mabrouk, Mohamed
2025.
Multiplicatively maximal numerical range-preserving maps.
Quaestiones Mathematicae,
p.
1.
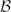 ${\mathcal B}$(X) (resp.
${\mathcal B}$(X) (resp. 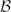 ${\mathcal B}$(Y)) be the algebra of all bounded linear operators on X (resp. on Y). For an operator T ∈
${\mathcal B}$(Y)) be the algebra of all bounded linear operators on X (resp. on Y). For an operator T ∈ 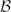 ${\mathcal B}$(X) and a vector x ∈ X, let σT(x) denote the local spectrum of T at x. For two nonzero vectors x0 ∈X and y0 ∈ Y, we show that a map ϕ from
${\mathcal B}$(X) and a vector x ∈ X, let σT(x) denote the local spectrum of T at x. For two nonzero vectors x0 ∈X and y0 ∈ Y, we show that a map ϕ from 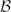 ${\mathcal B}$(X) onto
${\mathcal B}$(X) onto 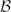 ${\mathcal B}$(Y) satisfiesif and only if there exists a bijective bounded linear mapping A from X into Y such that Ax0 = y0 and either ϕ(T) = ATA−1 or ϕ(T) = -ATA−1 for all T ∈
${\mathcal B}$(Y) satisfiesif and only if there exists a bijective bounded linear mapping A from X into Y such that Ax0 = y0 and either ϕ(T) = ATA−1 or ϕ(T) = -ATA−1 for all T ∈ 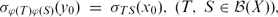 $\sigma_{\varphi(T)\varphi(S)}(y_0)~=~\sigma_{TS}(x_0),~(T,~S\in{\mathcal B}(X)),$
$\sigma_{\varphi(T)\varphi(S)}(y_0)~=~\sigma_{TS}(x_0),~(T,~S\in{\mathcal B}(X)),$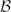 ${\mathcal B}$(X).
${\mathcal B}$(X).