Article contents
LOCALIZATIONS OF THE HEARTS OF COTORSION PAIRS
Published online by Cambridge University Press: 03 July 2019
Abstract
In this article, we study localizations of hearts of cotorsion pairs (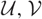 $\mathcal{U}, \mathcal{V}$) where
$\mathcal{U}, \mathcal{V}$) where 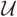 $\mathcal{U}$ is rigid on an extriangulated category
$\mathcal{U}$ is rigid on an extriangulated category 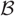 $\mathcal{B}$
. The hearts of such cotorsion pairs are equivalent to the functor categories over the stable category of
$\mathcal{B}$
. The hearts of such cotorsion pairs are equivalent to the functor categories over the stable category of 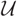 $\mathcal{U}$
(
$\mathcal{U}$
(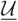 $\bmod \underline{\mathcal{U}}$
). Inspired by Marsh and Palu (Nagoya Math. J.225(2017), 64–99), we consider the mutation (in the sense of Iyama and Yoshino, Invent. Math.172(1) (2008), 117–168) of
$\bmod \underline{\mathcal{U}}$
). Inspired by Marsh and Palu (Nagoya Math. J.225(2017), 64–99), we consider the mutation (in the sense of Iyama and Yoshino, Invent. Math.172(1) (2008), 117–168) of 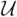 $\mathcal{U}$
that induces a cotorsion pair (
$\mathcal{U}$
that induces a cotorsion pair (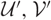 $\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$
). Generally speaking, the hearts of (
$\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$
). Generally speaking, the hearts of (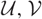 $\mathcal{U}, \mathcal{V}$
) and (
$\mathcal{U}, \mathcal{V}$
) and (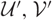 $\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$
) are not equivalent to each other, but we will give a generalized pseudo-Morita equivalence between certain localizations of their hearts.
$\mathcal{U}^{\prime}, \mathcal{V}^{\prime}$
) are not equivalent to each other, but we will give a generalized pseudo-Morita equivalence between certain localizations of their hearts.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © Glasgow Mathematical Journal Trust 2019
References
- 3
- Cited by


