Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-05T06:58:56.095Z Has data issue: false hasContentIssue false
  • English
  • Français

KMS states on 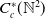$C_c^{*}(\mathbb{N}^2)$

Part of: Selfadjoint operator algebras Semigroups

Published online by Cambridge University Press:  03 April 2023

Anbu Arjunan ,
Sruthymurali  and
S. Sundar
Anbu Arjunan
Affiliation:
Indian Statistical Institute, Delhi Centre, NewDelhi, 110016, India
Sruthymurali
Affiliation:
Indian Statistical Institute, Bangalore Centre, Bangalore, 560059, India
S. Sundar*
Affiliation:
Institute of Mathematical Sciences (HBNI), Chennai, 600113, India
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 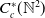$C_c^{*}(\mathbb{N}^{2})$ be the universal 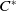$C^{*}$-algebra generated by a semigroup of isometries 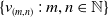$\{v_{(m,n)}\,:\, m,n \in \mathbb{N}\}$ whose range projections commute. We analyse the structure of KMS states on 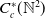$C_{c}^{*}(\mathbb{N}^2)$ for the time evolution determined by a homomorphism 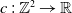$c\,:\,\mathbb{Z}^{2} \to \mathbb{R}$. In contrast to the reduced version 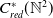$C_{red}^{*}(\mathbb{N}^{2})$, we show that the set of KMS states on 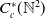$C_{c}^{*}(\mathbb{N}^{2})$ has a rich structure. In particular, we exhibit uncountably many extremal KMS states of type I, II and III.

Keywords

KMS statesSemigroupsGroupoids

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L30: States 20M99: None of the above, but in this section
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 65 , Issue 3 , September 2023 , pp. 501 - 528
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J, An introduction to infinite ergodic theory, Mathematical Surveys and Monographs, vol. 50 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Aaronson, J, Nakada, H, Sarig, O and Solomyak, R, Invariant measures and asymptotics for some skew products, Israel J. Math 128 (2002), 93–134.Google Scholar
Björklund, M, Z. Kosloff, and S. Vaes, Ergodicity and type of nonsingular Bernoulli actions, Invent. Math. 224(2) (2021), 573–625.Google Scholar
Brownlowe, N, Larsen, N. S., Ramagge, J and Stammeier, N, C $^{*}$ -algebras of right LCM monoids and their equilibrium states, Trans. Amer. Math. Soc. 373(7) (2020), 5235–5273.Google Scholar
Christensen, Johannes and Thomsen, Klaus, KMS states on the crossed product C $^{*}$ -algebra of a homeomorphism, Ergodic Theory Dynam. Syst. 42(4) (2022), 1373–1414.Google Scholar
Cuntz, J, C $^{*}$ -algebras associated with the $ax+b$ -semigroup over $\mathbb{N}$ , K-theory and noncommutative geometry, EMS Ser. Congr. Rep. (2008), 201–215. Available at https://mathscinet.ams.org/mathscinet/search/publications.html?fmt=bibtex&pg1=MR&s1=2513338 Google Scholar
Cuntz, J, Deninger, C and Laca, M, C $^{*}$ -algebras of Toeplitz type associated with algebraic number fields, Math. Ann 355(4) (2013), 1383–1423.Google Scholar
Cuntz, J, Echterhoff, S and Li, X, On the $K$ -theory of crossed products by automorphic semigroup actions, Q J. Math. 64(3) (2013), 747–784.Google Scholar
Cuntz, J and Li, X, The regular C*-algebra of an integral domain, Quanta of maths, Clay math. proc, vol. 11 (Amer. Math. Soc., Providence, RI, 2010), 149–170.Google Scholar
Cuntz, J and Li, X, C $^*$ -algebras associated with integral domains and crossed products by actions on adele spaces, J. Noncommut. Geom. 5(1) (2011), 1–37.Google Scholar
Danilenko, A. I. and Silva, C. E., Ergodic theory: non-singular transformations, Mathematics of complexity and dynamical systems, Vols. 1-3 (Springer, Newyork, 2012), 329–356.CrossRefGoogle Scholar
Hamachi, T, On a Bernoulli shift with nonidentical factor measures, Ergodic Theory Dynam. Syst. 1(3) (1981), 273–283, 1982.Google Scholar
Katznelson, Y., Sigma-finite invariant measures for smooth mappings of the circle, J. Anal. Math. 31 (1997), 1–18.Google Scholar
Laca, M and Neshveyev, S, Type $III_1$ equilibrium states of the Toeplitz algebra of the affine semigroup over the natural numbers, J. Funct. Anal. 261(1) (2011), 169–187.Google Scholar
Laca, M and Raeburn, I, Phase transition on the Toeplitz algebra of the affine semigroup over the natural numbers, Adv. Math. 225(2) (2010), 643–688.Google Scholar
Li, X, Semigroup C $^{*}$ -algebras and amenability of semigroups, J. Funct. Anal. 262(10) (2012), 4302–4340.Google Scholar
Li, X, Nuclearity of semigroup C $^{*}$ -algebras and the connection to amenability, Adv. Math. 244 (2013), 626–662.Google Scholar
Muhly, P. S. and Renault, J. N., C $^{*}$ -algebras of multivariable Wiener-Hopf operators, Trans. Amer. Math. Soc. 274(1) (1982), 1–44.Google Scholar
Murphy, G. J., C $^{*}$ -algebras generated by commuting isometries, Rocky Mountain J. Math. 26(1) (1996), 237–267.Google Scholar
Nakada, H, Piecewise linear homeomorphisms of type III and the ergodicity of cylinder flows, Keio Math. Sem. Rep. 7 (1982), 29–40. Available at https://mathscinet.ams.org/mathscinet/search/publications.html?fmt=bibtex&pg1=MR&s1=667804 Google Scholar
Nakada, H, On a classification of PL-homeomorphisms of a circle, Probability theory and mathematical statistics (Tbilisi, 1982), Lecture Notes in Math, vol. 1021 (Springer, Berlin, 1983), 474–480.Google Scholar
Neshveyev, S, KMS states on the C $^{*}$ -algebras of non-principal groupoids, J. Operator Theory 70(2) (2013), 513–530.CrossRefGoogle Scholar
Raeburn, I and Vittadello, S. T., The isometric representation theory of a perforated semigroup, J. Operator Theory 62(2) (2009), 357–370.Google Scholar
Salas, H. N., Semigroups of isometries with commuting range projections, J. Operator Theory 14(2) (1985), 311–346.Google Scholar
Sundar, S., C $^{*}$ -algebras associated to topological Ore semigroups, Münster J. Math. 9(1) (2016), 155–185.Google Scholar
Vittadello, S. T., The isometric representation theory of numerical semigroups, Integral Equations Operator Theory 64(4) (2009), 573–597.Google Scholar