Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T21:16:14.073Z Has data issue: false hasContentIssue false
  • English
  • Français

JACOBSON RADICAL ALGEBRAS WITH QUADRATIC GROWTH

Published online by Cambridge University Press:  01 October 2013

AGATA SMOKTUNOWICZ  and
ALEXANDER A. YOUNG
AGATA SMOKTUNOWICZ
Affiliation:
Maxwell Institute for Mathematical Sciences and School of Mathematics, University of Edinburgh, James Clerk Maxwell Building, King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, Scotland, United Kingdom e-mail: [email protected]
ALEXANDER A. YOUNG
Affiliation:
Department of Mathematics, University of California at San Diego, 9500 Gilman Drive, La Jolla, CA 92093-0112, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that over every countable algebraically closed field 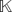$\mathbb{K}$ there exists a finitely generated 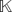$\mathbb{K}$-algebra that is Jacobson radical, infinite-dimensional, generated by two elements, graded and has quadratic growth. We also propose a way of constructing examples of algebras with quadratic growth that satisfy special types of relations.

Keywords

16N4016P90
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue A: New developments in Noncommutative Algebra and its applications. A conference in honour of Kenny Brown's and Toby Stafford's 60th birthdays. , October 2013 , pp. 135 - 147
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Bartholdi, L., Branch rings, thinned rings, tree enveloping rings, Israel J. Math. 154 (2006), 93–139.Google Scholar
2.Krause, G. R. and Lenagan, T. H., Growth of algebras and Gelfand-Kirillov dimension, Revised ed., Graduate Studies in Mathematics, 22. (American Mathematical Society, Providence, RI, 2000).Google Scholar
3.Lenagan, T. H. and Smoktunowicz, A., An infinite dimensional algebra with finite Gelfand–Kirillov algebra, J. Amer. Math. Soc. 20 (4) (2007), 989–1001.CrossRefGoogle Scholar
4.Lenagan, T. H., Smoktunowicz, A. and Young, A. A., Nil algebras with restricted growth, Proc. Edinburgh Math. Soc. (Ser. 2), 55 (2012), 461–475.Google Scholar
5.Small, L. W., Stafford, J. T. and Warfield, R. B. Jr., Affine algebras of Gelfand–Kirillov dimension one are PI, Math. Proc. Camb. Philos. Soc. 97 (3) (1985), 407–414.Google Scholar
6.Smoktunowicz, A., Jacobson radical algebras with Gelfand–Kirillov dimension two over countable fields, J. Pure Appl. Algebra 209 (3) (2007), 839–851.Google Scholar
7.Smoktunowicz, A. and Bartholdi, L., Images of Golod–Shafarevich algebras with small growth, Q. J. Math. First published online (2013) doi:10.1093/qmath/hat005.Google Scholar
8.Smoktunowicz, A. and Bartholdi, L., Jacobson radical non-nil algebras of Gelfand-Kirillov dimension 2, Israel J. Math 194 (2) (2013), 597–608.Google Scholar
9.Vishne, U., Primitive algebras with arbitrary Gelfand-Kirillov dimension, J. Algebra 211 (1) (1999), 150–158.Google Scholar