Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T08:38:16.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrals involving hypergeometric functions and E-functions

Published online by Cambridge University Press:  18 May 2009

T. M. Macrobert
T. M. Macrobert
Affiliation:
The University Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In § 2 a number of integrals in which the integrand contains a product of a hypergeometric function and an E-function will be evaluated. The following formulae will be employed in the proofs.

If ρ +σ = α + β + γ + 1, and if α, β or γ is zero or a negative integer,

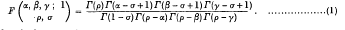
this is Sallschütz's theorem [1].

If R(γ - ½α - ½β)< - ½,

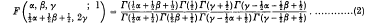
This theorem was given by Wastson [2] for negative integral values of α and later by Whipple [3] for general values α.

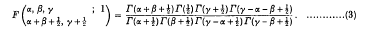
R(γ) > 0,

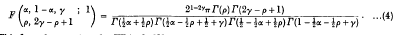
This formula was given by Whipple [3]

l is a positive integer,

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 3 , Issue 4 , July 1958 , pp. 196 - 198
Copyright
Copyright © Glasgow Mathematical Journal Trust 1958

References

REFERENCES

1.Saalschütz, L., Zeitschrift für Math. u. Phys., 35 (1890), 186–188; 36 (1891), 278–295, 321–327.Google Scholar
2.Watson, G. N., Proc. London Math. Soc. (2), 23 (1923), XIII–XV.Google Scholar
3.Whipple, F. J. W., Proc. London Math. Soc. (2), 23 (1923), 104–114.Google Scholar