Article contents
Integrals involving E-functions
Published online by Cambridge University Press: 18 May 2009
Extract
In this paper three integrals involving E-functions are evaluated in terms of E-functions. The formulae to be established are:
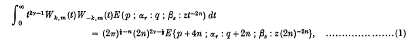
where n is a positive integer, | args z < π, R(γ ± m ÷ ½) > 0, αρ+ν = (2γ + ν)/2n (ν = 1, 2, …, 2n), αρ+2n+i = (γ + m - ½ + i)/n, αρ+3n+i = (γ - m - ½ + i)/n, βα+i = (γ + κ + i)/n, βα+ν+i = (γ - κ + i)/n(i = 1, 2, …, n).
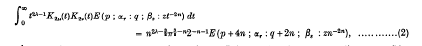
where n is a positive integer, |arg z| < π, R(λ±μ±ν) > 0, αp+i+1 = (λ + μ + ν + i)/n, αp+n+i+1 = (λ - μ + ν + i)/n, αp+2n+i+1 = (λ + μ - ν + i)/n, αp+3n+i+1 = (λ - μ - ν + i)/n (i = 0, 1, 2, …, n - 1), βa+i+1 = (2λ + j)/2n (j = 0, 1, 2, …, 2n - 1).
where n is a positive integer, R(λ) > ½, |arg z| < π, αp+i+1 = (2λ - 1 + i)/2n (i = 0, 1, 2, …, 2n-1), βq+j+1 = (λ + μ j)/n, βq+n+j+1 = (λ - μ + j)/n (j = 0, 1, 2, …, n-1).
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1960
References
- 2
- Cited by


