In § 2 a number of infinite series of E-functions are summed by expressing the E-functions as Barnes integrals and interchanging the order of summation and integration.

The Barnes integral employed is

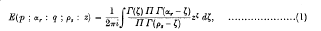
where | amp z | < π and the integral is taken up the η;-axis, with loops, if necessary, to ensure that the origin lies to the left of the contour and the points α1, α2,… αp to the right of the contour. Zero and negative integral values of the α's and p's are excluded, and the α's must not differ by integral values. When p < q + 1 the contour is bent to the left at each end.