Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T17:14:17.006Z Has data issue: false hasContentIssue false
  • English
  • Français

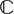HYPERSURFACES IN ${\mathbb C}$P2 AND 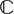${\mathbb C}$H2 WITH TWO DISTINCT PRINCIPAL CURVATURES

Part of: Global differential geometry General theory in ordinary differential equations

Published online by Cambridge University Press:  21 July 2015

THOMAS A. IVEY  and
PATRICK J. RYAN
THOMAS A. IVEY
Affiliation:
Department of Mathematics, College of Charleston, 66 George St., Charleston, SC, USA e-mail: [email protected]
PATRICK J. RYAN
Affiliation:
Department of Mathematics and Statistics, McMaster University, Hamilton, ON, Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

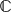It is known that hypersurfaces in ${\mathbb C}$Pn or 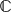${\mathbb C}$Hn for which the number g of distinct principal curvatures satisfies g ≤ 2, must belong to a standard list of Hopf hypersurfaces with constant principal curvatures, provided that n ≥ 3. In this paper, we construct a two-parameter family of non-Hopf hypersurfaces in 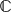${\mathbb C}$P2 and 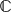${\mathbb C}$H2 with g=2 and show that every non-Hopf hypersurface with g=2 is locally of this form.

MSC classification

Primary: 53C40: Global submanifolds
Secondary: 34A99: None of the above, but in this section
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 1 , January 2016 , pp. 137 - 152
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Berndt, J., Real hypersurfaces with constant principal curvatures in complex hyperbolic space, J. Reine Angew. Math. 395 (1989), 132–141.Google Scholar
2.Díaz-Ramos, J. C. and Domínguez-Vázquez, M., Non-Hopf real hypersurfaces with constant principal curvatures in complex space forms, Indiana Univ. Math. J. 60 (2011), 859–882.CrossRefGoogle Scholar
3.Díaz-Ramos, J. C., Domínguez-Vázquez, M. and Vidal-Castiñeira, C., Real hypersurfaces with two principal curvatures in complex projective and hyperbolic planes, arXiv preprint 1310.0357v1 [math.DG].Google Scholar
4.Ivey, T. A., A d'Alembert formula for Hopf hypersurfaces, Results Math. 60 (2011), 293–309.CrossRefGoogle Scholar
5.Ivey, T. A. and Landsberg, J. M., Cartan for Beginners: Differential geometry via moving frames and exterior differential systems (American Mathematical Society, Providence, RI, 2003).Google Scholar
6.Kimura, M., Real hypersurfaces and complex submanifolds in complex projective space, Trans. Amer. Math. Soc. 296 (1986), 137–149.CrossRefGoogle Scholar
7.Montiel, S., Real hypersurfaces of a complex hyperbolic space, J. Math. Soc. Japan 37 (1985), 515–535.CrossRefGoogle Scholar
8.Niebergall, R. and Ryan, P. J., Real hypersurfaces in complex space forms, in Tight and taut submanifolds (Chern, S.-S. and Cecil, T. E., Editors) (MSRI Publications, Cambridge, UK, 1997), 233–305.Google Scholar
9.Takagi, R., On homogeneous real hypersurfaces in a complex projective space, Osaka J. Math. 10 (1973), 495–506.Google Scholar
10.Takagi, R., Real hypersurfaces in a complex projective space with constant principal curvatures, J. Math. Soc. Japan 27 (1975), 43–53.Google Scholar
11.Warner, F. W., Foundations of differentiable manifolds and Lie groups (Springer-Verlag, New York-Berlin, 1983).CrossRefGoogle Scholar