Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vavilov, N. A.
and
Stepanov, A. V.
2013.
Linear groups over general rings. I. Generalities.
Journal of Mathematical Sciences,
Vol. 188,
Issue. 5,
p.
490.
Randal-Williams, Oscar
and
Wahl, Nathalie
2017.
Homological stability for automorphism groups.
Advances in Mathematics,
Vol. 318,
Issue. ,
p.
534.
Sprehn, David
and
Wahl, Nathalie
2020.
Homological stability for classical groups.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 7,
p.
4807.


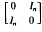 . The main result of this paper is the following theorem.
. The main result of this paper is the following theorem.