Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T01:37:53.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic inverse semigroups

Published online by Cambridge University Press:  18 May 2009

Mario Petrich  and
Stuart A. Rankin
Mario Petrich
Affiliation:
University of Western Ontario, London, Canada
Stuart A. Rankin
Affiliation:
University of Western Ontario, London, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An inverse semigroup S shall be said to be harmonic if every congruence on S is determined by any one of its classes. In other words, if λ and ρ are congruences on S having a congruence class in common, then λ = ρ. The class 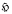of all harmonic semigroups contains all bisimple inverse semigroups, as proved by Žitomirskiĭ [11] and also by Schein [10], and all congruence-free inverse semigroups. Moreover, 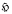is contained in the class of all 0-simple or simple inverse semigroups, as is easy to see. We shall show that there exist non-bisimple, non-congruence-free harmonic semigroups and that there are simple inverse semigroups which are not harmonic.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 3 , September 1989 , pp. 335 - 351
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Ash, C. J., Dense, uniform and densely subuniform chains, J. Austral. Math. Soc. Ser. A 23 (1977), 1–8.CrossRefGoogle Scholar
2.Hall, T. E., Congruences and Green's relations on regular semigroups, Glasgow Math. J. 13 (1972), 167–175.Google Scholar
3.Koch, R. J., Comparison of congruences on regular semigroups, Semigroup Forum 26 (1983), 295–305.CrossRefGoogle Scholar
4.Lallement, G. and Petrich, M., Décompositions I-matricielles d'un demi-groupe, J. Math. Pures Appl. 45 (1966), 67–117.Google Scholar
5.Munn, W. D., Congruence-free inverse semigroups, Quart. J. Math. Oxford Ser. (2) 25 (1974), 463–484.CrossRefGoogle Scholar
6.Petrich, M., Inverse Semigroups (Wiley-Interscience, 1984).Google Scholar
7.Petrich, M. and Rankin, S. A., Congruences induced by transitive representations of inverse semigroups, Glasgow Math. J. 29 (1987), 21–40.Google Scholar
8.Rankin, S. A., Congruences on an inverse Bruck-Reilly semigroup: Part I. Non-group congruences, preprint.Google Scholar
9.Reilly, N. R., Congruence-free inverse semigroups, Proc. London Math. Soc. Ser. (3) 33 (1976), 497–514.Google Scholar
10.Schein, B. M., A remark concerning congruences on (O-)bisimple inverse semigroups, Semigroup Forum 3 (1971), 80–83.CrossRefGoogle Scholar
11.Žitomirskiĭ, G. I., On imprimitivity relations of generalized groups of transformations, (in Russian), Mat. Sb. (N.S.) 73 (1967), 500–512.Google Scholar